Пусть группа

содержит меньше

элементов. Тогда
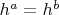
для каких-то

таких что

. Что тогда можно сказать про порядок

?

- порождающий элемент конечной группы

. Его порядок равен числу элементов в группе

, т.е. он будет меньше

.
-- 16.07.2021, 00:21 --Кажется, скомпилировалось. Рассмотрим

. Она будет подгруппой группы

. Она содержит

элементов, а значит, она будет совпадать с

, чтд.