Спасибо, пасьянс сошёлся. Всё получается очень красиво, если начинать не с набора из

функций

, а сразу с функции

.
Напомним определение случайной величины. Рассмотрим пространство

с заданной на нем сигма-алгеброй

. Рассмотрим также вероятностное пространство

. Случайной величиной

называется

-измеримая функция
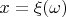
, определенная на

и принимающая значения из

.
Если за

принять

, мы получим обычную (одномерную) случайную величину. Взяв в качестве

пространство

, получим

-мерную случайную величину или

-мерный случайный вектор.
Теорема. Пусть

- случайная величина

, заданная на вероятностном пространстве

. Тогда её координатные функции

сами являются случайными величинами

, заданными на том же вероятностном пространстве. Обратно, упорядоченный набор из

случайных величин

, заданных на одном и том же вероятностном пространстве

, образует координатные функции случайного вектора

, заданного на том же вероятностном пространстве. При определении случайных величин сигма-алгебры на

и

приняты борелевскими.
Это непосредственно следует из следующей леммы.
Лемма. Пусть

- борелевская сигма-алгебра на

,

- борелевская сигма-алгебра на

,

- произвольная сигма-алгебра на

. Функция

является

-измеримой, согда все её координатные функции


-измеримы.
Таким образом, под

-мерной случайной величиной можно понимать упорядоченный набор из

случайных величин

, заданных на одном и том же вероятностном пространстве

, который также называется системой случайных величин. Интуитивный смысл этого определения прост: в результате одного и того же испытания свои значения принимают

случайных величин (например, координаты выбранной точки).