Забудем про

и рассмотрим переходящие друг в друга пары

, как точки на координатной плоскости

. Мне так привычнее.
1) Дискриминант

, откуда

. Кроме того, по условию

, кроме самой первой точки (а мы пока забудем про самую первую, в самом конце вспомним). Тут, конечно, хорошо бы представить себе это пересечение этих двух множеств на координатной плоскости, мне лень рисовать. Пересечение состоит из двух изолированных частей, у одной из них

, у второй
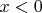
(точка

запрещена условием!). Первую часть назовём 1A, вторую — 1B.
2) Будем пытаться определить "разрешённую" область точек на

, которая остаётся "разрешённой" максимальное число шагов (а вдруг даже бесконечное?), отрезая по кусочкам "запрещённые" части. Часть координатной плоскости мы уже "запретили" на шаге 1), ибо два шага переживают только точки 1A и 1B.
3) Двигаемся в противоположную сторону:

по формулам Виета:

, причём на каждом шаге (кроме последнего, ну, то есть, в терминах задачи — первого) должно выполняться условие

.
4) Имеем:

, или

. Представили себе это множество, да? Гипербола

, сдвинутая вниз и влево на 1, её две ветви разбивают плоскость на 3 части, разрешёнными из них являются две выпуклые, в одной из которой координаты строго
положительны больше -1, во второй — строго отрицательны. Первая часть пересекается с 1A (пересечение назовём 2A, хотя оно совпадает с 1A) вторая — с 1B (пересечение назовём 2B). (мысленно) нарисуем себе это пересечение. Это та область, которая переживает три шага.
5) У 2B обе координаты отрицательны. При преобразовании Виета они переходят в (обе) положительные, т.е. есть шанс попасть в 2A. В то время как положительные элементы 2A при преобразовании переходят в область, в которой

, т.е. в запрещённую. Итак, только элементы 2B переживают 4 шага алгоритма, но не более.
Наверное, нужно привести пример, свидетельствующий, что 4-шаговые последовательности существуют?

, корни

и

(проверяем теоремой Виета)

, корни

и

(лежат в области 1A=2A)

, корни

и

(лежат в области 2B)

, корни

и


, нет корней