Здравствуйте.
Читаю "Дифференциальную геометрию: Первое знакомство" Э. Позняка. Есть пример: кривая

гладкая в любой своей точке, но никакая окрестность точки
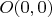
не является гладкой кривой.
Наша кривая осциллирует при малых

, а в точке

терпит интуитивно понимаемый разрыв. Но пользуясь определениями в той же книге я не могу себе этого наглядно представить.
Если кривая гладкая в каждой своей точке, то в каждой такой точке существует касательная и некоторая окрестность каждой точки кривой однозначно проектируется на эту касательную. Кривая называется гладкой, если она является гладкой в каждой точке и касательные в точках кривой изменяются непрерывно. 1-е условие для нашей кривой выполняется, значит не выполняется 2-е, то есть, касательные не меняются непрерывно. Если например кривая имеет излом, то кривая не будет гладкой поскольку она не будет гладкой в точке излома и понятно, что касательная не будет непрерывно менятся. Значит у нашей кривой какая-то другая особенность, которую я не могу визуализировать.