Воспользоваться теоремой Лагранжа

[artempalkin]

Это одна из задач из Кудрявцева

Воспользовавшись теоремой Лагранжа, доказать сравнение

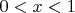
$x^{\alpha}|\ln x|$ и $\frac 1{\alpha e}$ (что-то должно быть больше, а что-то меньше, видимо) при $0<x<1$ и $\alpha>0$.

В общем, как я не перекидываю множители и слагаемые из одной части в другую, не находится у меня нужное выражение. Я пытался т. Лагранжа применить двумя способами к функции $x^{\alpha}$, считая аргументами разные буквы:

$x^{\alpha}-1=x^{\xi}\ln x \cdot \alpha$

$x^{\alpha}=\alpha \eta^{\alpha-1}x$,

но что-то не приводит это к ответу. Может, нужно использовать другую функцию? В особенности я не могу понять, откуда вытащить $e$, которое есть в ответе

[mihaild]

artempalkin в сообщении #1507811 писал(а):

Это одна из задач из Кудрявцева

А можно точнее? Формулировка выглядит странно (и скажем что тут понимается под теоремой Лагранжа?).

artempalkin в сообщении #1507811 писал(а):

что-то должно быть больше, а что-то меньше

А вы подставьте скажем $x = \frac{1}{e}$ и посмотрите, что будет при разных $\alpha$.
UPD: это я обсчитался, всё нормально.

[artempalkin]

mihaild в сообщении #1507824 писал(а):

А можно точнее? Формулировка выглядит странно (и скажем что тут понимается под теоремой Лагранжа?).

Первый том, 16 глава, 15 (5) (стр 312 в моем издании)

Там, видимо, опечатка в условии (опять же, в моем издании). Так что есть шанс, что условие вообще другое.

[svv]

Разве что пропущен знак неравенства: $x^\alpha|\ln x|\leqslant 1/(\alpha e)$ при $0<x<1,\alpha>0$.
А с 15(3) нет проблем? Тогда в $e^t\geqslant 1+t$ подставьте $t=-\ln (x^\alpha) - 1$.

[artempalkin]

svv в сообщении #1507829 писал(а):

А с 15(3) нет проблем? Тогда в $e^t\geqslant 1+t$ подставьте $t=-\ln (x^\alpha) - 1$.

Да, тогда все получается. Я пробовал вытащить оттуда $e$, тоже $-1$ использовал, но до ответ не дошел. Спасибо большое :)