Внешние формы и тензоры

[arseniiv]

StaticZero в сообщении #1499151 писал(а):

А можно я глупые вопросы пока позадаю? Аргумент функции -- вектор, а почему градиент будет именно 1-формой, а не вектором?

Можно любые вопросы!

Тут если мы будем рассматривать многообразия — и рассмотрим линейное пространство как многообразие, у которого все касательные пространства совпадают с им самим, то аргумент функции будет вектором, да, но в общем случае точкой многообразия. Если же мы рассматриваем просто одно линейное пространство, как само по себе, то скалярное поле это просто один скаляр и всё (в противовес скаляру в каждой точке многообразия). Физики любят звать поле со значениями вида А и одну штуку вида А одинаково «А», так что скаляр может быть скалярным полем или отдельным скаляром, и особенно это касается $n$-форм, потому что вроде не принято говорить «вектор» про целое поле.

Дальше, я остерегусь говорить «градиент», потому что по-моему это действительно вектор, который есть в (псевдо)римановом случае и есть просто результат свёртки дифференциала с метрическим тензором, в общем вектор, канонически сопоставленный 1-форме. 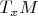В общем случае никакого градиента у нас не будет: исходная функция у нас идёт из многообразия $M$ в $\mathbb R$, и дифференциал её в каждой точке $x$ — это линейное отображение из $T_x M$, касательного пространства в этой точке, в $T_{f(x)} \mathbb R$, касательное к $\mathbb R$. Последнее — всегда то же самое что и само $\mathbb R$, так что мы получаем $T_x M \to \mathbb R$, линейное отображение из векторов в скаляры, то есть ковектор, притом это всё так и зависит от точки до сих пор, и в разных точках у нас разные касательные пространства.

(Но если мы возьмём аффинное или векторное пространство, то да, у нас везде будет одно и то же касательное пространство, потому что аффинное пространство плоское. Больше нигде так не везёт. Но пусть такое упрощение нас не смущает.)

-- Вт янв 05, 2021 23:23:10 --

StaticZero в сообщении #1499160 писал(а):

Пока не вижу, как эту святую простоту согласовать с новым ковекторным языком.

Тут будет просто. Когда мы представили ковектор упорядоченной парой гиперплоскостей, а вектор стрелочкой, то мы можем представить применение одного к другому как ответ на вопрос, сколько раз стрелочка помещается между парой плоскостей. В частности если стрелочку можно целиком уложить на гиперплоскость, результат 0, и если можно сделать, чтобы она начиналась на первой плоскости и кончалась на второй, то 1, а если в обратную сторону, то −1. Так можно вообразить два двойственных базиса как некую конструкцию в виде коробки.

Когда на сцену выходит скалярное произведение (которое нужно чтобы получить градиент из дифференциала), мы получаем способ конвертации векторов в ковекторы и обратно, но какой? Тут будет тоже полезно посмотреть на скалярное произведение, а точнее на соответствующую квадратичную форму, как уровни. Для евклидова пространства это будут концентрические гиперсферы (или эллипсы, если мы сомневаемся в себе), для псевдоевклидова всякие гипергиперболоиды (брр!) двух типов и конус, разграничивающий их. Конец каждого вектора утыкается при этом в такую гиперсферу, касательная гиперплоскость к которой в этой точке как раз ортогональна этому вектору именно в том смысле, в котором говорит выбранное нами скалярное произведение. Таким образом мы можем на картинке для любого вектора $\mathbf v$ найти ковектор, дающий ноль для любых ортогональных $\mathbf v$ векторов. Его лишь немного масштабировать — и мы найдём ковектор $\mathbf v^\flat$ такой, чтобы скалярное произведение $(\mathbf v, \mathbf w)$ было ровно тем же, что и просто применение $(\mathbf v^\flat, \mathbf w)$.

Для евклидова скалярного произведения мы знаем, что если $(\mathbf e, \mathbf w) = (\mathbf e, \mathbf e) = 1$, то $(\mathbf w, \mathbf w) \geqslant 1$, и притом $\mathbf w = \mathbf e$ — единственный случай, когда будет равенство; аналогично если требовать $(k, \mathbf w) = (k, k) = 1$ для ковектора $k$, то равенство будет при $\mathbf w = k^\sharp$, вектору, сопоставленному $k$ скалярным произведением; так что в евклидовом случае мы получим, что соответствующий дифференциалу вектор направлен в направлении скорейшего возрастания функции (мы хотим соединить две гиперповерхности уровня наикратчайшим вектором). Не уверен что хорошо объясняю.

[StaticZero]

Уххх...

Если градиент это всё-таки вектор, то откуда тогда берётся представление об 1-форме как о плоскостях? Кого мы выпрямляем и в какой точке? Вот я стою на склоне двумерного многообразия $M$, и в этой точке можно найти касательную плоскость $TM$ и некоторую соответствующую изолинию, но одну. Откуда вторая?

А что означают бемоли и диезы? У меня есть догадка, но смутная, вовлекающая в себя "опускание-поднятие" индексов.

[arseniiv]

StaticZero в сообщении #1499225 писал(а):

Кого мы выпрямляем и в какой точке?

Можно сказать, бесконечно близкие поверхности уровня. Чем они ближе, тем быстрее функция меняется, тем больше дифференциал, и направлен в направлении изменения, хотя оно теперь «нормально» направлено — и фокус независимости этого от скалярного произведения как раз в том, что ортогональность двух векторов или двух ковекторов мы можем лишь с ним, а «ортогональность» вектора и ковектора — без! Имея дифференциал, мы можем узнать направления, в которых функция не меняется, они будут как раз лежать в той же плоскости, что задаётся бесконечно близкими бесконечно маленькими поверхностями уровня в интересующей точке.

StaticZero в сообщении #1499225 писал(а):

Откуда вторая?

Нам нужна вторая, чтобы показать величину. Исходно для иллюстрации мы берём поверхности уровней, отличающиеся на 1, например, или там на $1/1000$, и берём любые две соседние, но тогда и умножаем полученное расстояние в $1000$ раз. И чем ближе возьмём уровни, тем прямее маленькие кусочки поверхностей уровня в окрестности точки, ну и в пределе получим картинку с плоскостями, из которых мы оставили для удобства только две, а не все. А вообще отдельный ковектор — это ведь линейная функция, и если нарисовать две её плоскости уровней в линейном пространстве векторов, то мы получим как раз ту рафинированную картинку; уровни должны быть 0 и 1, или там −1 и 0 (тут уже важно, чтобы уровни отличались на 1, чтобы правило «вектор на ковектор даёт количество откладываний вектора, умещающееся между плоскостями» работало). Это я вам ещё не успел рассказать как их графически складывать, и наконец перейти к 2-формам и всяким там операциям, хотя надо для начала будет разобрать случай двумерного линейного пространства, может и двумерного многообразия заодно.

StaticZero в сообщении #1499225 писал(а):

А что означают бемоли и диезы? У меня есть догадка, но смутная, вовлекающая в себя "опускание-поднятие" индексов.

Да! Это способ записать без индексов именно это. Выписывая отдельно от контекста:
$\mathbf v^\flat$ — это ковектор, определяемый как $(\mathbf v^\flat, \mathbf u) = (\mathbf v, \mathbf u)$, где справа скалярное произведение. Это ровно то же что и сказать, что $(\mathbf v^\flat)_i = g_{ij} v^j$, так как свернув с $u^i$, получим $(\mathbf v^\flat)_i u^i = g_{ij} v^j u^i$, ну разве что я попутал местами то, с каким индексом $g$ что сворачивается, но как мы знаем, $g_{ij} = g_{ji}$.

Аналогично:
$k^\sharp$ — это вектор, определяемый как $(k^\sharp, \mathbf u) = (k, \mathbf u)$ (также мы можем использовать действие на ковекторах и скалярное произведение на них, индуцированное скалярным произведением векторов). Опять же это будет ровно то же что и сказать $(k^\sharp)^i = g^{ij} k_j$; ну или ладно, $(k^\sharp)^i g_{ij} = k_j$; это одно и то же, потому что $g^{ij} g_{j\ell} = \delta^i {}_\ell$.

[StaticZero]

Я тут наткнулся на вот какую проблему. Пусть у нас есть замена векторного базиса

$$ \mathbf h_j = {S^k}_j \mathbf e_k. $$

Обратное будет иметь вид

$$ {S_q}^j \mathbf h_j = {S_q}^j {S^k}_j \mathbf e_k = {\delta_q}^k \mathbf e_k = \mathbf e_q $$

Для координат векторов получаем:

$$ \tilde x^i \mathbf h_i = x^i \mathbf e_i = x^i {S_i}^j \mathbf h_j, \qquad \tilde x^j = {S_i}^j x^i. $$

Векторы преобразуются по обратной матрице $S^{-1}$ в то время, как базисные векторы преобразовывались по закону $\mathbf h_i = S \mathbf e_i$, это контравариантный способ. С другой стороны, замена ковекторного базиса

$$ \mathsf h^j(\mathbf x) = \mathsf h^j(x^i \mathbf e_i) = x^i {S_i}^k \mathsf h^j(\mathbf h_k) = x^i {S_i}^k {\delta^j}_k = {S_i}^j x^i = {S_i}^j \mathsf e^i(\mathbf x), $$

так что $\mathsf h^j = {S_i}^j \mathsf e^i$, откуда ${S^k}_j \mathsf h^j = \mathsf e^k$ и для координат ковекторов получаю

$$ \tilde x_i \mathsf h^i = x_k \mathsf e^k = x_k {S^k}_i \mathsf h^i, \qquad \tilde x_i = {S^k}_i x_k $$

и получается, что ковекторные координаты преобразуются так же, как и векторные, хотя должно быть $\tilde x_i = {S_i}^k x_k$, чтобы получался ковариантный способ. Что я делаю не так?

[arseniiv]

Я для этого использую те же буквы, но индексы разной штрихованности для разных базисов. Тогда если

$$\mathbf e_{j'} = \mathbf e_j S^j {}_{j'}$$

(на самом деле $S^j {}_{j'} = \delta^j {}_{j'}$ — натуральная дельта — единичный оператор, записанный просто в двух разых базисах с разных сторон; при желании мы так можем записывать и другие операторы, но это всех запутает) и если обратное (обозначу с немного другим порядком индексов, чем у вас)

$$\mathbf e_{j'} S'^{j'} {}_j = \mathbf e_j S^j {}_{j'} S'^{j'} {}_j = \mathbf e_j \delta^j {}_j$$

(и $S'$ тоже дельта была, откуда дополнительно ясно, что они при умножении дадут тоже дельту,* если бы мы вдруг забыли, что этого и хотели; дальше всё пишу дельтами). Для координат тогда

$$\mathbf x = \mathbf e_{j'} x^{j'} = \mathbf e_j \delta^j {}_{j'} x^{j'} = e_j x^j \quad\Longrightarrow\quad \delta^j {}_{j'} x^{j'} = x^j$$

(пытался я какой-то логический порядок множителей выбрать и что-то здесь он стал совсем уж обратный, хм).

Теперь для ковекторов я бы делал как-то так:

$$(\mathsf k, \mathbf x) = k_j x^j = k_j \delta^j {}_{j'} x^{j'} = k_{j'} x^{j'} \quad\Longrightarrow\quad k_j \delta^j {}_{j'} = k_{j'}$$

или

$$k_j = k_{j'} \delta^{j'} {}_j$$

а уж после координат можно потрогать и сам двойственный базис:

$$\mathsf k = k_j \mathsf e^j = k_{j'} \delta^{j'} {}_j \mathsf e^j = k_{j'} \mathsf e^{j'} \quad\Longrightarrow\quad \delta^{j'} {}_j \mathsf e^j = \mathsf e^{j'}$$

и тут всё аккуратно получилось, ну или там повращать немного дельты туда-сюда, чтобы было прозрачнее.

После этого можно такие штуки писать механически, потому что штрихи помогают вместе с различением верхних и нижних индексов разрешить лишь корректные записи (если как обычно допускать сворачивать лишь лишь одинаковые индексы — с учётом и штрихов).**

_______
* Потому что для общего случая произведение операторов в координатах в трёх потенциально разных базисах $(AB)^i {}_{k''} = A^i {}_{j'} B^{j'} {}_{k''}$, и с дельтами и всего двумя разными базисами выйдет, что мы перемножили два тождественных оператора и получили такой снова: $\delta^i {}_{j'} \delta^{j'} {}_{k} = \delta^i {}_k$, и раз справа точно уже единичная матрица, то две матрицы слева обратны друг другу.

** Штрихи и подобные пометки ещё могут вместо разных базисов в одном пространстве обозначать нам даже разные пространства, хотя для настолько различающихся индексов $i, \tilde\jmath$ у нас уже больше не будет осмысленной величины $\delta^i {}_{\tilde\jmath}$.

[StaticZero]

Дельта???

Да, топик стал сложным, над вкуривать неспеша...

[пианист]

StaticZero в сообщении #1499258 писал(а):

Что я делаю не так?

StaticZero в сообщении #1499258 писал(а):

должно быть $\tilde x_i = {S_i}^k x_k$

[StaticZero]

Разобрал пример с поворотом. Стало ясно: если я использую замену $\mathbf h_i = S \mathbf e_i$, то тогда автоматически $\mathsf h^i = S \mathsf e^i$, что как раз и даёт одинаковый вид преобразования ковариантных и контравариантных компонент (тогда получается в этих названиях нет никакого смысла).

-- 06.01.2021 в 13:25 --

Теперь кажется более понятным, что писал arseniiv. Дельта имеется в виду в том смысле, что закон преобразования выбран так, чтобы получалось:

новый базисный вектор с номером $k$ = матрица перехода $\times$ старый базисный вектор с номером $k$

и другие базисные векторы не примешиваются ни слева, ни справа. Но в виде дельт это трудно воспринять

[Утундрий]

Я, конечно, понимаю, что раздел математический, но из темы стремительно улетучивается всякий смысл. Мню, больше будет толку от рассмотрения конкретных примеров непонятных

StaticZero в сообщении #1499121 писал(а):

тексты "физика+топология"

[arseniiv]

StaticZero в сообщении #1499282 писал(а):

Дельта???

Ага, матрица перехода это матрица единичного оператора, так что мне лично приятнее её обозначать дельтой. Как только мы перестаём использовать сразу несколько разных базисов в формулах, всё это можно забыть.

-- Ср янв 06, 2021 19:55:28 --

(Вот кстати а в связи двойственных базисов $\mathbf e_i \mathsf e^j = \delta_i {}^j$ что за дельта? Но это философский вопрос, эту тему им загромождать не будем.)

[StaticZero]

arseniiv в сообщении #1499241 писал(а):

двумерного многообразия заодно.

Ну вот я пытаюсь через холмик понимать.

Вложение:

dxdy_contour.png [ 49.03 Кб | Просмотров: 0 ]

Здесь изолинии вроде бы расставлены как раз через равные промежутки.

Вот я могу встать в точку, где проведена изолиния; локально это отрезок прямой. Следующая будет проходить через другие точки. Я могу выбрать направление, вдоль которого я иду по холму. Вот я по нему иду-иду и дохожу до следующей изолинии. В новой точке тоже получаю локально отрезок. Эти два отрезка находятся в параллельных двумерных изоплоскостях-сечениях (эти плоскости тоже находятся на расстоянии 1, поскольку мы выбрали изолинии уровней, отличающихся на 1), но линии, их содержащие, в общем случае скрещиваются (меня вот сбивало с толку, о плоскостях какой размерности вы говорите ).

Если я иду с единичной скоростью в заданном направлении (направление задаётся в касательной плоскости вектором скорости, здесь он длины 1, а прямая, содержащая этот вектор, проектируется на холмик в некоторую кривую, вдоль которой я отсчитываю пройденное расстояние), то я достигну следующей изолинии через время $t_0$. Если я удвою скорость, то время будет $t_0/2$. Если я поменяю направление, но оставлю единичный модуль, то будет какое-то другое время $t_1$ и т. д., так что я прихожу к образу 1-формы как функционала времени путешествия до следующей изолинии в зависимости от направления и величины скорости.

Вы это имели в виду?

-- 06.01.2021 в 20:52 --

Хотя нет, такое описание сталкивается с трудностью. Если я иду вдоль $x$ с единичной скоростью, то я достигну следующей изолинии за время $t_x$, а вдоль $y$ -- за время $t_y$, и для согласования с условием $\mathsf e^i(\mathbf e_j) = {\delta^i}_j$ нужно, чтобы характерные масштабы времени $t_x$ и $t_y$ были разными (либо "единичная скорость в направлении" была назначена так, чтобы время в соответствующем направлении до следующей изолинии было всегда 1, что мне нравится больше)...

[arseniiv]

Всё равно вроде хорошая картина. Главное не забывать, что мы иллюстрируем не изолинии исходной функции, а изолинии её линейной части.

StaticZero в сообщении #1499389 писал(а):

Эти два отрезка находятся в параллельных двумерных изоплоскостях-сечениях (эти плоскости тоже находятся на расстоянии 1, поскольку мы выбрали изолинии уровней, отличающихся на 1)

(Ага, это вы уже на графике функции гуляете, так можно будет и запутаться.)

[StaticZero]

Нашёл книжку несколько чище, чем Ефимов: Tu. Introduction to Manifolds. Её уважаемый vpb уже упоминал на форуме (так я её и нашёл, собственно).

[vpb]

StaticZero в сообщении #1499555 писал(а):

уже упоминал на форуме (так я её и нашёл, собственно).

Что-то я этого эпизода не помню ... А Ефимов книжка хорошая.

[StaticZero]

(Оффтоп)

vpb в сообщении #1500514 писал(а):

Что-то я этого эпизода не помню

Ууууууу... Я посмотрел сейчас, оказывается, двух ЗУ перепутал как-то Это был уважаемый Slav-27.