Здравствуйте все, я зашел в тупик при решении этой задачи, хочу попросить совет, как двигаться дальше. Спасибо!
Вот задача:
Функции Лагранжа
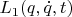
и
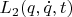
порождают тождественные уравнения.
Показать, что эти функции отличаются на
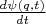
, где
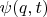
- произвольная функция.
Попытка решения:
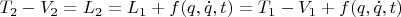
, где
- кинетические энергии.
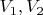
- обобщенные потенциалы.
Отсюда следует, что
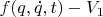
тоже обобщенный потенциал. Пусть
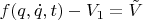
.
Обобщенная сила

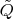
не зависит от ускорений
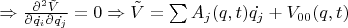
. Т.к.
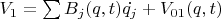
,
то
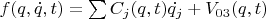
. Получилось, что

линейна по обобщенным скоростям,
но как связать это с тем, что она есть полная производная какой-то произвольной функции

по времени я не знаю.