Теорема Пуанкаре о возвращении

[sergey zhukov]

Теорема Пуанкаре о возвращении говорит в частности о том, что если фазовая точка $X$ гамильтоновой консервативной системы, фазовое пространство которой компактно и имеет конечный объем, стартует в момент времени $0$ из точки $X(0)$, то существует такое время $t$, когда она обязана вернуться в сколь угодно малую окрестность одной из точек своей траектории $X(0)...X(t)$.

Эта теорема основана на возможности уложить без самопересечения лишь конечное число фазовых объемов $V(X(0))$ окрестности точки $X(0)$ в полном конечном фазовом объеме системы $V$. Можно сказать, что возвращение фазовой точки в окрестность какой-либо точки собственной прошлой траектории $X(0)...X(t)$ становится неизбежным, как только обьем всего фазового пространства $V$ оказывается покрыт непересекающимися обьемами, равными обьему окрестности $V(X(0))$ (если же они пересекаются, то, значит, возвращение произошло еще раньше).

Правильно ли я понимаю, что если упростить, то эта теорема говорит о следующем: как только система исчерпала все конечное множество вариантов своего состояния, на следующем шаге она неизбежно перейдет в одно из своих предыдущих состояний? Например, если мы бросаем кость шесть раз и не получили ни одного повторения, то на седьмой мы точно получим возвращение к одному из предыдущих шести состояний?
И еще: возвращение не обязательно происходит в окрестность точки $X(0)$? Доказывается, что фазовая траектория с началом в точке $X(0)$ обязательно попадет в окрестность какой-то одной из своих собственных точек $X(m)$. Потом мы переносим $X(0)$ на место $X(m)$ и говорим, что неизбежность возврата системы в точку $X(m)$ доказана.

[Aritaborian]

Лихо вы упростили эту теорему до принципа Дирихле.

[sergey zhukov]

Aritaborian
Принцип Дирихле ведь в основе ее доказательства?

[Aritaborian]

Боюсь, что всё не так просто.

[novichok2018]

Aritaborian - согласен. Не видел, чтобы тут применялся элементарный принцип Дирихле. Давно, когда учился, мне оказалась полезной и интересной очень хорошо написанная книга:
Дж. Окстоби. Мера и категория. (Есть на лыжах). Там есть понятное обсуждение теоремы Пуанкаре в отдельной главе. Там много чего используется: мера, категория, теоремы Бэра и Банаха и тд. Если интересно - посмотрите.

[sergey zhukov]

Aritaborian
Вот, например, в этом видео https://youtu.be/hGbmwYZaV18 теорема Пуанкаре о возвращении доказывается так:

1. Пусть у нас есть отображение $g$ такое, что оно непрерывно, однозначно и с сохранением объема отображает множество $A$ в себя. Множество $A$ пусть имеет конечный обьем;

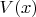
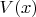
2. Возьмем точку $x$ множества $A$ и некоторую малую ее окрестность объема $V(x)$. Отображение $g$ однозначно и обратимо переводит эту окрестность $V(x)$ в некоторую другую окрестность равного обьема $V(x)\to g(V(x))$. Если применить отображение еще раз, то получим $g(V(x)) \to g^2(V(x))$ и т.д. $g^n(V(x))$ - это $n$-ый шаг применения отображения $g$ к объему окрестности $V(x)$.

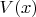
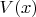
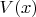
3. Очевидно, что применяя это отображение снова и снова, мы постепенно заполняем конечный объем множества $A$ отображениями $V(x)$. Из-за конечности объема множества $A$, а так же из-за сохранения на каждом шаге объема отображения $V(x)$ этот процесс неизбежно должно привести к пересечению цепи отображений самой с собой как минимум после того, как весь объем $A$ будет исчерпан. Примерно как в известной компьютерной игре, в которой удлиняющийся удав должен в конце-концов наткнуться на собственное тело, т.к. свободного места уже не остается. Допустим, что пересеклись отображения с номером $2$ и $8$:

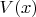
Здесь для простоты $g$ не меняет формы объема $V(x)$, чтобы непрерывность и сохранение объема были очевиднее.

4. Теперь, оказывается, что нарисованное невозможно. Почему? Потому, что т.к. отображение $g$ однозначно, то оно обратимо. Значит, можно применить это отображение в обратную сторону к точкам красной области пересечения. Но т.к. эти точки одновременно принадлежат отображениям $g^2(V(x))$ и $g^8(V(x))$, то при обратном отображении они одновременно должны перейти и в $g^1(V(x))$ и в $g^7(V(x))$, которые у нас не пересекаются. Вывод - они на самом деле пересекаются, т.е. пересечение должно было произойти как минимум еще между $g^1(V(x))$ и $g^7(V(x))$. Применяя это рассуждение многократно для общего случая, заменив конкретные $2$ и $8$ на $k$ и $m$, всегда можно прийти к выводу, что на самом деле конец цепи всегда должен пересечься с ее началом на шаге $g^{m-k}(V(x))$. Т.е. удав должен уткнуться не куда-нибудь, а именно в конец своего хвоста.

5. Вот и все. Мы имеем такой результат:

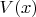
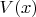
Если взять любую точку из красной области (звездочка) и проследить ее перемещение в обратном направлении, то она вернется в окрестность $V(x)$. Мы получили точку такую, которая, стартуя из окрестности $V(x)$ вновь гарантированно попадает в нее на шаге $g^{m-k}(V(x))$. Сама точка $x$ тут никакой роли не играет.

По моему, в доказательстве этой теоремы самое главное - это свойства отображения $g$ - непрерывность, взаимная однозначность и сохранение объема, а так же конечность объема множества $V$. Трудно, вероятно, доказать, что именно такое отображение $g$ описывает движение точки механической системы в фазовом пространстве. Сама же теорема о возвращении кажется довольно простой и не требует ничего, кроме принципа Дирихле.

[Aritaborian]

sergey zhukov в сообщении #1494343 писал(а):

По моему, в доказательстве этой теоремы самое главное - это свойства отображения $g$ - непрерывность, взаимная однозначность и сохранение объема, а так же конечность объема множества $V$. Трудно, вероятно, доказать, что именно такое отображение $g$ описывает движение точки механической системы в фазовом пространстве. Сама же теорема о возвращении кажется довольно простой и не требует ничего, кроме принципа Дирихле.

Насколько я спосбен понять из этих слов, вы утверждаете, что в доказательстве теоремы есть некий трудный момент, но его можно обойти и выбросить. Но не показываете, как.

[sergey zhukov]

Aritaborian
Теорема Пуанкаре о возвращении - это теорема о некотором множестве и некотором отображении на этом множестве. И у этого отображения есть некоторые специальные свойства. Вот это вроде бы несложно и изложено выше.

Но нужно ведь еще показать, что все это имеет отношение к описанию механических систем. Это уже за пределами собственно теоремы о возвращении. Но об этой теореме обычно вспоминают именно в приложении ее к механическим системам. Вот об этом выше ничего не сказано и это, возможно, труднее самой теоремы о возвращении.

[Padawan]

sergey zhukov в сообщении #1494343 писал(а):

Мы получили точку такую, которая, стартуя из окрестности $V(x)$ вновь гарантированно попадает в нее на шаге $g^{m-k}(V(x))$. Сама точка $x$ тут никакой роли не играет.

Точно сформулируйте теорему Пуанкаре о возвращении. Есть разные версии этой теоремы.

[v_n]

sergey zhukov
А мне непонятно, что вообще такое "объем фазового пространства гамильтоновой консервативной системы". Можете пояснить чему он равен и как его вычислить для а) одномерного осциллятора и б) трехмерного осциллятора. Хоть я и не понимаю как вычисляется объем мне почему-то кажется, что во втором случае он будет равен нулю.

[sergey zhukov]

Padawan
Вот как эта теорема формулируется в указанном видео. Допустим, у нас есть множество $A$ конечного объема и отображение $g$, переводящее $A$ в себя такое, что $g$ взаимно-однозначно, непрерывно и сохраняет объем. Тогда для любой точки $x$ в любой ее окрестности $V(x)$ найдется такая точка $x_0$, что многократное (некоторое $n$-кратное) отображение этой точки $g^n(x_0)$ снова попадает в окрестность $V(x)$.

v_n
Я это так понимаю. Консервативная система, имеющая энергию $E$, может находиться только в определенных точках фазового пространства, соответствующих этой энергии. Геометрическое место всех таких точек образует объем, который должен быть конечен.
Например, система из трех гравитирующих тел отображается точкой в 18-мерном фазовом пространстве. Закон сохранения энергии системы трех тел накладывает одно ограничение на движение этой точки, в результате точка движется по 17-мерной изоэнергетической поверхности $E$, вложенной в 18-мерное фазовое пространство. Площадь этой поверхности должна быть конечна.
Нулевая площадь такой поверхности? По моему, этого не может быть. Если у системы есть какие-то степени свободы и какая-то энергия, то у нее есть и конечная площадь поверхности, соответствующая этой энергии, по которой она движется.

[v_n]

sergey zhukov в сообщении #1495518 писал(а):

Закон сохранения энергии системы трех тел накладывает одно ограничение на движение этой точки, в результате точка движется по 17-мерной изоэнергетической поверхности $E$, вложенной в 18-мерное фазовое пространство. Площадь этой поверхности должна быть конечна.

С этим вполне можно согласиться, но я не знаю теорем о сохранении 17-мерной площади при эволюции данной гамильтоновой системы. Зато знаю теорему Лиувилля о сохранении 18-мерного объема при эволюции. А 18-мерный объем 17-мерной изоэнергетической поверхности таки равен нулю.

[Padawan]

sergey zhukov в сообщении #1495518 писал(а):

Padawan
Вот как эта теорема формулируется в указанном видео. Допустим, у нас есть множество $A$ конечного объема и отображение $g$, переводящее $A$ в себя такое, что $g$ взаимно-однозначно, непрерывно и сохраняет объем. Тогда для любой точки $x$ в любой ее окрестности $V(x)$ найдется такая точка $x_0$, что многократное (некоторое $n$-кратное) отображение этой точки $g^n(x_0)$ снова попадает в окрестность $V(x)$.

А я такую версию теоремы Пуанкаре знаю: если отображение $f$ сохраняет меру, то для любой точки $x$, за исключением точек некоторого множества нулевой меры, и для любой окрестности $V(x)$ точки $x$ существует бесконечно много номеров $n$ таких, что $f^n(x)\in V(x)$.
По-моему, это отличается от того, что Вы написали.

[Ben]

v_n в сообщении #1494757 писал(а):

sergey zhukov
А мне непонятно, что вообще такое "объем фазового пространства гамильтоновой консервативной системы".

Мне кажется, в этой фразе присутствует 2 независимых понятия. Объем фазового пространства мы выделяем сами, приписывая всем независимым переменным приращения dx dy dz dp_x dp_y dp_z. На основании уравнений движения выпускаем из нашего объема траектории и смотрим как деформируется кубик.

А где в теореме Пуанкаре спрятано требование к "перемешиванию"? Что мешает траектории описывать устойчивый цикл? В этом случае система точно не будет стремиться заполнить весь фазовый объем.