Непонятно только почему Вы считаете это Пеллем.
Существуют ли параметры

, при которых уравнения Пелля
1).

2).

имеют решение.
При фиксированных параметрах будем иметь обобщённые уравнения Пелля. (Пропустила слово обобщённые? Учту.)
несколько искусственное условие

Согласна. Но пока пусть будет.
Хотелось бы подробнее рассмотреть второе уравнение относительно существования решения в зависимости от последней цифры у параметра
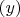
.
2).

У меня получилось, что, если решение существует, то

должны быть нечётными. Тогда рассмотрим, каким должно быть

, чтобы решение существовало. Получим:
1).

,

не существует
2).

, возможные последние цифры

3).

, возможные последние цифры

4).

, возможные последние цифры

5).

,

не существует
Остались не рассмотренными два случая (если я не ошиблась в остальных):
2).

, возможные последние цифры

3).

, возможные последние цифры

Т.е. надо выяснить, существует ли решение, если параметр
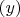
оканчивается на цифры

. При существовании решение найдётся перебором. А если не существует? В любом случае будет интересно посмотреть, как на самом деле.