Определите молярную теплоемкость азота

, расширяющегося по закону

В этой задаче у меня проблема больше с математической частью. Теплоемкость можно найти по формуле

, в свою очередь Q можно найти по формуле
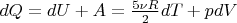
. Вот тут мне не очень понятно, как действовать. Нам дан закон, из которого можно получить функции V(T) и T(V). Как это использовать при решении задачи? Можете, пожалуйста, показать, каким образом тут нужно дифференцировать.