Ньютоновское искривление траектории света

[profilescit]

This part is concerned with the effect of a gravitational field on the propagation of light in space.

(a) A photon emitted from the surface of the Sun (mass $M$, radius $R$) is red-shifted. By assuming a rest-mass equivalent for the photon energy, apply Newtonian gravitational theory to show that the effective (or measured) frequency of the photon at infinity is reduced (red-shifted) by the factor $\left ( 1 - \frac{GM}{R c^2}\right )$
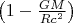
(b) A reduction of the photon's frequency is equivalent to an increase in its time period, or, using the photon as a standard clock, a dilation of time. In addition, it may be shown that a time dilation is always accompanied by a contraction in the unit of length by the same factor.
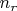
We will now try to study the effect that this has on the propagation of light near the Sun. Let us first define an effective refractive index $n_r$ at a point $r$ from the centre of the Sun. Let
$n_r = \frac{c}{c'}$
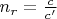
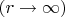
where $c$ is the speed of light as measured by a co-ordinate system far away from the Sun's gravitational influence $(r \to \infty)$, and $c'$ is the speed of light as measured by a co-ordinate system at a distance $r$ from the centre of the Sun.
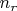
Show that $n_r$ may be approximated to:
$n =1+\frac{2GM}{r c^2}$

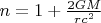
Моя попытка решения:
(a) Чтобы узнать эффективную массу фотона, приравняем его энергию к релятивистской энергии $h \nu = m c^2$ а значит $ m = \frac{h \nu}{c^2}$
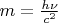
Закон сохранения энергии $h \nu - \frac{G M m}{R} = h \nu'$
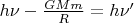
откуда $\nu' = \nu \left ( 1 - \frac{GM}{R c^2}\right ) $

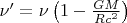
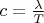
(b) $c = \frac{\lambda}{T}$ а значит, согласно тексту (время уменьшается а расстояние увеличивается, и наоборот), $ c' = \frac{\lambda'}{T'}$
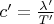
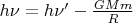
Из того же сохранения энергии получаем что $h \nu = h \nu' - \frac{GMm}{R}$ а значит $\nu' = \nu \left ( 1 + \frac{GM}{r c^2}\right )$ откуда $T' = \frac{T}{\left ( 1 + \frac{GM}{r c^2}\right )}$
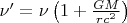
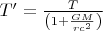
Откуда получим что $ c' = c \left ( 1 + \frac{GM}{r c^2}\right )^2$
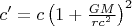
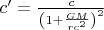
против $ c' = \frac{c} {\left ( 1 + \frac{GM}{r c^2}\right )^2}$ в ответе.

В чем заключается ошибка?

[Pphantom]

Первая строчка в решении (b) непонятно откуда следует. Что интересно, из нее сразу же делается вывод, прямо противоречащий результату (a) - вас это не смущает?

[profilescit]

Не противоречит, ведь в первом пункте мы находим частоту в бесконечности через частоту около Солнца. Во втором пункте мы находим частоту около Солнца через частоту в бесконечности.

[Pphantom]

Тогда напишите решение аккуратнее. В исходном тексте обозначения со штрихом или без оного были привязаны к совершенно конкретным условиям, а вы, похоже, это не заметили.

P.S. Кстати, штрих мне пришлось поправить - он был набран каким-то неотображающимся символом.

[profilescit]

И все же ошибку найти не могу...
Перепишем выражение частоты около Солнца через частоту в бесконечности $\nu ' = \nu \left ( 1 + \frac{GM}{r c^2}\right )$
По тексту задачи, длина будет умножена на тот же фактор а значит $\lambda ' = \lambda \left ( 1 + \frac{GM}{r c^2}\right )$

$c = \nu \lambda$ а значит $\frac{\Delta c}{c} = \frac{\Delta \lambda}{\lambda} + \frac{\Delta \nu}{\nu}$

Где $\Delta \lambda = \lambda \left ( \frac{GM}{r c^2}\right )$, $\Delta \nu = \nu \left ( \frac{GM}{r c^2}\right ) $

Тогда $\frac{c' - c}{c} = \frac{2GM}{r c^2}$, получая тот же ответ $c ' = c \left ( 1 + \frac{2 G M}{r c^2} \right )$

[Pphantom]

profilescit в сообщении #1494054 писал(а):

Перепишем выражение частоты около Солнца через частоту в бесконечности $\nu ' = \nu \left ( 1 + \frac{GM}{r c^2}\right )$

И каким образом этот результат согласуется с результатом пункта (a)?

[sergey zhukov]

profilescit
Я бы так решал:

Часы, наблюдаемые из бесконечности и находящиеся на расстоянии $r$ от центра массы идут так $t_r=t_0(1+\frac{\varphi}{c^2})$, где $\varphi$ - гравитационный потенциал в точке $r$, а $t_0$ - показания часов удаленного наблюдателя. Соответственно, $dt_r=dt_0(1+\frac{\varphi}{c^2})$

Метр в точке нахождения этих часов по условию задачи должен соотносится с метром наблюдателя, как $dx_r=\frac{dx_0}{1+\frac{\varphi}{c^2}}$

Тогда координатная скорость света $c^\prime$ в точке $r$ равна $c^\prime =\frac{dx_r}{dt_r}=\frac{dx_0}{dt_0} \frac{1}{(1+\frac{\varphi}{c^2})^2}=c \frac{1}{(1+\frac{\varphi}{c^2})^2}$

$\frac{1}{(1+\frac{\varphi}{c^2})^2} \approx 1-\frac{2\varphi}{c^2}$, поэтому $\frac{c^\prime}{c}=1-\frac{2\varphi}{c^2}=1+\frac{2MG}{rc^2}$

[profilescit]

Pphantom в сообщении #1494058 писал(а):

И каким образом этот результат согласуется с результатом пункта (a)?

В пункте а мы нашли частоту света в бесконечности выражая через частоту около Солнца
В пункте б я нахожу частоту света около Солнца выражая через частоту в бесконечности

Пусть $\nu_{солнце}$ и $\nu_{\infty}$ будут эти соответствующие частоты.

Тогда согласно пункту а $\nu_{\infty} = \nu_{солнце} (1 - \frac{GM}{R c^2})$
И согласно пункту b $\nu_{солнца} = \nu_{\infty} (1 + \frac{GM}{R c^2})$ что прекрасно согласовывается в виду малости выражения $\frac{GM}{R c^2}$

sergey zhukov так я ведь такой-же ответ получаю, а в задаче говорят что другой надо получить

[Pphantom]

profilescit в сообщении #1494060 писал(а):

В пункте а мы нашли частоту света в бесконечности выражая через частоту около Солнца
В пункте б я нахожу частоту света около Солнца выражая через частоту в бесконечности

В задаче все нештрихованные величины относятся к положению на бесконечности (скорость, частота и т.д.), а штрихованные - к положению около Солнца. В частности, то же самое относится и к ответам, приводимым автором задачи. Вы же меняете обозначения в процессе решения, как следствие, в результате получается каша, которую бессмысленно с чем-либо сравнивать.

Так что первое, что тут нужно сделать: аккуратно написать решение, для самого себя зафиксировав, что каким образом обозначается.

[sergey zhukov]

profilescit
Тут видимо так нужно решать.

В точке $r$ местные часы идут со скоростью $dt_r=dt_0(1+\frac{\varphi}{c^2})$, а местный метр равен $dx_r=\frac{dx_0}{1+\frac{\varphi}{c^2}}$. Скорость света при измерении местыми масштабами всегда должна быть равна $c$, поэтому $c=\frac{dx_0}{dt_0} \frac{1}{(1+\frac{\varphi}{c^2})^2}$. А $\frac{dx_0}{dt_0}$ - это скорость света в точке $r$, измеренная масштабами удаленного наблюдателя, которая и равна $c^\prime=\frac{dx_0}{dt_0}$. Поэтому мы и получаем $c=c^\prime \frac{1}{(1+\frac{\varphi}{c^2})^2}$ $\frac{c}{c^\prime}=1-\frac{2\varphi}{c^2}=1+\frac{2MG}{rc^2}$