Достать 5 шаров из 15 можно

способами
Первый шаг и сразу на мину, хехе.

Биномиальный коэффициент показывает вам что? Изначально он произошёл из перестановок. Смотрите. У вас пять шаров с номерами 1..5. Вам их надо расставить на полке. Вы можете выбрать шарик, который будет стоять первым, пятью способами. Вы его выбрали и поставили. В руке осталось четыре. Четыре именно, а не пять, здесь нет возвращений. Дальше понятно, перемножаем всё подряд, получаем
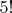
.
Теперь вам говорят: "ладно, расставьте не пять шаров, а три из пяти". Как и прежде, вы рассуждаете: я на первое место шар выберу пятью способами; ...; на третье место выберу тремя способами; мне сказали поставить только три шара, на этом всё". Перемножаете

. Зададим переменную

. Предыдущему случаю соответствовало

. Нынешнему, формально,

.
Теперь вам говорят: "поставьте три из пяти, номера сотрите". Вы такой: а как учесть стёртость номеров? Товарищи математики вам говорят: ну давайте
сначала расставим три с любыми циферками, а потом оставшиеся перестановки трёх шаров просто отождествим. В итоге получается:
-

шаров

способами
- взять из них

пронумерованных

способами
- взять из них

без номеров: предыдущее число

нужно ещё разделить на перестановки

шаров в количестве

, так что в итоге

.
Обратите внимание, что здесь нигде нет возвращения шаров. Самое большое из этих чисел -- число перестановок -- уже получено исходя из того, что ушедший шар из набора ушёл с концами. Остальные числа ещё меньше и соответствуют дополнительным накладываемым ограничениям (неполное взятие; неполное взятие с игнорированием порядка).
Нетрудно догадаться, что схема с возвращением -- это степень. Например, у вас есть пять лунок специальных под шары, в руке пять чистых шаров и маркер. Сколькими способами вы можете заполнить лунки нумерованными шарами, если дозволяется на каждом шаре писать любое число 1..5 (независимо от того, что написано на остальных)? Это

.
Отсюда до схемы Бернулли рукой подать.