последовательность же состоит из попарно различных точек по построению
Ну да. Это бесконечное множество, которое по условию имеет предельную точку. Но я не понимаю почему эта точка является предельной точкой последовательности. Ведь это разные определения:
1) Предельная точка (

) множества - точка, в любой окрестности которой найдется хотя бы одна точка множества, отличная от

.
2) Предельная точка последовательности - предел какой-либо подпоследовательности.
Как я понимаю, 2 автоматически не следует из 1. Пример: какая-то окрестность точки содержит конечное число точек множества, все, в этом случае предельной точкой последовательнсти она быть не может.
А условий, при которых она являлась бы предельной точкой последовательности (
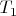
), насколько я понимаю, в теореме не требуют.
-- 14.10.2020, 20:31 -- то есть можно построить последовательность точек, которые сходятся к предельной точке множества значений.
Как?
-- 14.10.2020, 20:40 --Кажется я смутно начинаю догадываться. Берем любую окрестность

точки

, в ней выбираем точку множества

, затем берем любую другую окрестность

, строим ее пересечение с

:

и в нем выбираем точку множества

и так далее. Если какая-то окрестность будет содержать в себе любую окрестность из постренной системы окрестностей то она будет содержать и все точки последовательности, начиная с некоторой. Однако этого недостаточно чтобы последовательность сходилась к исходной точке

. Надо чтобы это свойство выполнялось для любой окрестности. В общем чего-то тут не хватает.