Комментарии к "Векторным уравнениям плоскости.." Беклемишева

[Vladimir Pliassov]

Комментируются фрагменты п.4 § 2 гл.II учебника Беклемишева «Курс аналитической геометрии и линейной алгебры» "Векторные уравнения плоскости и прямой".

Ссылка на файл с этой книгой, которым я располагаю, к сожалению, не работает, но это известный учебник Беклемишева, его при желании можно найти по интернету.

В кавычках стоят выдержки из учебника.

"П р е д л о ж е н и е 5. Пусть $x, y, z$ - компоненты вектора $r$ в декартовой системе координат. Тогда скалярное произведение $(r-r_0, n)$ при $n \ne 0$ записывается линейным многочленом $Ax+By+Cz+D \,\,\, (A^2+B^2+C^2 \ne 0)$.

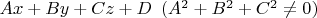Обратно, для любого линейного многочлена найдутся такие векторы $r_0$ и $n \ne 0$, что в заданной системе координат $Ax+By+Cz+D=(r-r_0, n)$.

Первая часть предложения очевидна: подставим разложение вектора $r$ по базису в данное нам выражение

$$(xe_1+ye_2+ze_3-r_0, \,\,n),$$

раскроем скобки и получим многочлен $Ax+By+Cz+D$, в котором $D=-(r_0, \,\, n)$ и

$$A=(e_1, \,\,n), \,\,B=(e_2, \,\,n), \,\,C=(e_3, \,\,n). \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(13)$$

$A,B,C$ одновременно не равны нулю, так как ненулевой вектор $n$ не может быть ортогонален всем базисным векторам."

Если бы вектор $n$ был ортогонален всем базисным векторам $(e_1,e_2,e_3)$, он сам мог бы быть базисным вектором - четвертым базисным вектором, то есть пространство, в котором доказывается П р е д л о ж е н и е 5 , было бы не трехмерным, а четырехмерным.

"Для доказательства обратного утверждения найдем сначала вектор $n$ из равенств (13), считая $A,B$ и $C$ заданными. Будем искать этот вектор в виде

$$n=\alpha [e_2, e_3]+\beta [e_3, e_1]+\gamma[e_1, e_2].$$

Умножив скалярно это равенство на $e_1$, получаем $(e_1, \,\,n)=\alpha (e_1,e_2,e_3).$"

(При умножении $[e_3, e_1]$ и $[e_1, e_2]$ на $e_1$ получаются нули.)

"Отсюда ..."

... поскольку $A=(e_1, \,\,n)$

"... $\alpha=A/(e_1,e_2,e_3)$.

Аналогично находим $\beta$ и $\gamma$."

При этом, когда ищем $\beta$, принимаем во внимание, что

"Для любых векторов $a,b$ и $c$ мы получаем, сравнивая ориентации троек векторов,

$$(a,b,c)=(c,a,b)=(b,c,a)...

(Беклемишев «Курс аналитической геометрии и линейной алгебры», стр.24-25)

так что

$$(e_2, \,\,[e_3, e_1])=(e_2, e_3, e_1)=(e_1, e_2, e_3)$$

и

$$(e_2, \,\,n)=\beta (e_2, e_3, e_1)=\beta (e_1, e_2, e_3).$$

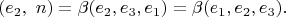
Поскольку $B=(e_2, \,\,n), \,\,C=(e_3, \,\,n)$, имеем $\beta=B/(e_1,e_2,e_3),\,\,\gamma=C/(e_1,e_2,e_3)$.

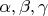
Подставим полученные значения $\alpha, \beta, \gamma$ в

$$n=\alpha [e_2, e_3]+\beta [e_3, e_1]+\gamma[e_1, e_2],$$

получим

$$n=A \frac {[e_2, e_3]}{(e_1,e_2,e_3)}+B \frac {[e_3, e_1]}{(e_1,e_2,e_3)} +C \frac{[e_1, e_2]}{(e_1,e_2,e_3)}.$$

Так как

$$\frac {[e_2, e_3]}{(e_1,e_2,e_3)}=e_1^\star, \,\,\, \frac {[e_3, e_1]}{(e_1,e_2,e_3)}=e_2^\star, \,\,\, \frac{[e_1, e_2]}{(e_1,e_2,e_3)}=e_3^\star,$$

где $e_1^\star, e_2^\star, e_3^\star$ векторы базиса, взаимного с базисом $e_1, e_2, e_3,$ (см. Беклемишев. «Курс аналитической геометрии и линейной алгебры», стр.32), то

$$n=A e_1^\star+B e_2^\star +C e_3^\star.$$

Таким образом, мы искали вектор $n$ в виде

$$\alpha [e_2, e_3]+\beta [e_3, e_1]+\gamma[e_1, e_2],$$

а нашли еще и в виде

$$A e_1^\star+B e_2^\star +C e_3^\star.$$

"Вектор $n$ не нулевой, так как $[e_2, e_3],[e_3, e_1]$ и $[e_1, e_2]$ линейно независимы (предложение 7 § 3 гл.1), а $\alpha, \beta$ и $\gamma$ не равны нулю одновременно, так же как $A,B$ и $C$."

Вектор $n$ не нулевой также и потому, что $e_1^\star, e_2^\star, e_3^\star$ линейно независимы и $A,B,C$ не равны нулю одновременно.

Поскольку вектор $n$ имеет по базису $e_1^\star, e_2^\star, e_3^\star$ координаты $A,B,C$, а вектор $r$ по базису $e_1,e_2,e_3$ имеет координаты $x,y,z$, и при этом базисы $e_1,e_2,e_3$ и $e_1^\star, e_2^\star, e_3^\star$ взаимные, то

$$(r,\,\,n)=(xe_1+ye_2+ze_3, \,\,\, A e_1^\star+B e_2^\star +C e_3^\star)=xA+yB+zC.$$

(Таблица умножения векторов взаимных базисов представляет собой единичную матрицу, например, в данном случае

$$(e_1, e_1^\star)=\langle e_1, \,\frac {[e_2, e_3]}{(e_1,e_2,e_3)}\rangle=\frac {1}{(e_1,e_2,e_3)}(e_1, [e_2, e_3])=\frac {(e_1,e_2,e_3)}{(e_1,e_2,e_3)}=1,$$

а

$$(e_1, e_2^\star)=\langle e_1, \,\frac {[e_3, e_1]}{(e_1,e_2,e_3)}\rangle=\frac {1}{(e_1,e_2,e_3)}(e_1, [e_3, e_1])=\frac {0}{(e_1,e_2,e_3)}=0.)$$

"Итак,"

[учитывая, что

$$A=(e_1, \,\,n), \,\,B=(e_2, \,\,n), \,\,C=(e_3, \,\,n)]$$

"мы можем придать заданному многочлену..."

(то есть многочлену

$$Ax+By+Cz+D=xA+yB+zC+D)$$

"...вид

$$x(e_1,\,\,n)+y(e_2,\,\,n)+z(e_3,\,\,n)+D=(r,\,\,n)+D.

Далее,

"П р е д л о ж е н и е 6. Если система координат декартова прямоугольная, то вектор с компонентами $A,B$ и $C$ является нормальным вектором для плоскости $Ax+By+Cz+D=0$."

То есть, если система координат не прямоугольная, то вектор $n$ не может иметь по базису $e_1, e_2, e_3$ координаты $A,B,C$, эти координаты по базису $e_1, e_2, e_3$ имеет какой-то другой вектор, но не $n$, об этом другом векторе у автора вообще не идет речь в доказательстве П р е д л о ж е н и й 5, 6.

Тем не менее рассматриваемая плоскость имеет выражение $Ax+By+Cz+D=0$, и $A,B,C$ являются координатами нормального вектора $n$, но по базису $e^\star_1, e^\star_2, e^\star_3$:

"В случае общей декартовой системы координат"

(то есть необязательно прямоугольной)

$ - компоненты вектора $n$ по базису $e^\star_1, e^\star_2, e^\star_3$, взаимному с $e_1, e_2, e_3$."

Правильно?

[Nemiroff]

В чём состоит вопрос? Вы переписываете учебник, потом спрашиваете, правильно ли вы переписали?

[Vladimir Pliassov]

Nemiroff в сообщении #1484248 писал(а):

В чём состоит вопрос? Вы переписываете учебник, потом спрашиваете, правильно ли вы переписали?

То, что из учебника, стоит в кавычках, остальное мое.

[Lia]

Vladimir Pliassov
:( Теги quote к Вашим услугам в этом случае. В следующий раз. Сейчас уже вряд ли успеете.

[Nemiroff]

Vladimir Pliassov в сообщении #1484251 писал(а):

То, что из учебника, стоит в кавычках, остальное мое.

Всё ещё: в чём ваш вопрос?
Разложение $\mathbf{n}$ по взаимному базису написано в этой самой книжке. В зависимости от издания: либо явно, либо со ссылкой на параграф.

[Vladimir Pliassov]

Nemiroff в сообщении #1484253 писал(а):

Vladimir Pliassov в сообщении #1484251 писал(а):

То, что из учебника, стоит в кавычках, остальное мое.

Всё ещё: в чём ваш вопрос?
Разложение $\mathbf{n}$ по взаимному базису написано в этой самой книжке. В зависимости от издания: либо явно, либо со ссылкой на параграф.

В этой самой книжке, но не на этой странице. Автор, как и многие другие авторы, не злоупотребляет подробностями.

Я долго не мог понять, но потом как будто понял и спрашиваю, правильно ли понял.

[Vladimir Pliassov]

Lia в сообщении #1484252 писал(а):

Vladimir Pliassov
:( Теги quote к Вашим услугам в этом случае. В следующий раз. Сейчас уже вряд ли успеете.

Нашел ссылку, может быть, не самую лучшую, но все же.

https://docviewer.yandex.ru/view/0/?*=7 ... 3D&lang=ru