Две таблицы — это как?
Поясню.
Для начала, нужно воздать должное студентам и таки вывести формулу Ньютона для вычисления обратного корня. :)
Допустим, мы хотим найти значение "x" при котором обращается в нуль функция f(x) заданная выражением:

Очевидно, что эта функция равна нулю как раз при

Чтобы воспользоваться формулой Ньютона, вычислим производную функции f(x):

Откуда находим формулу для итераций:

Пусть вещественное положительное число "a" представлено в нормализованном формате с плавающей запятой:

, причем, нам известно, что

Представим число "a" в виде:

или:

Причем:

Выберем начальное значение

для итерационной формулы Ньютона в виде:

Тогда для первой итерации находим значение

в виде:

Или:

Или:

Тогда для относительной ошибки
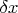
первой итерации находим оценку:

Или:

То есть, для выбранной величины

одной итерации Ньютона достаточно для вычисления корня с одинарной точностью float..
...
Теперь снова вернемся к итерационной формуле Ньютона и воспользуемся двумя таблицами для вычисления начальных значений величин

и

Рассмотрим сначала случай четного "N".
Для вычисления

нам нужна таблица значений величин:
Код:
float f1[4096];
for (int n = 0; n < 4096; n++) f1 = 1.5f / sqrt(1.0f + (float)n/4096);
Для индексирования элементов в этой таблице мы будем использовать двоичные числа:

Само значение

при этом вычисляется по формуле:

Для вычисления

нам нужна таблица значений величин:
Код:
float f2[4096];
for (int n = 0; n < 4096; n++) f2 = 0.5f / sqrt((1.0f + (float)n/4096)*(1.0f + (float)n/4096)*(1.0f + (float)n/4096));
Для индексирования элементов в этой таблице мы также будем использовать двоичные числа:

Само значение

при этом вычисляется по формуле:

Теперь формула для вычисления

сводится к одному умножению и одному сложению:

Еще одно умножение потребуется чтобы из

получить

:

...
Для случая нечетных "N" вычисления делают аналогично, с той лишь разницей, что нужно использовать индексы:

и вместо массивов f1 и f2 использовать массивы:
Код:
float f3[4096];
for (int n = 0; n < 4096; n++) f3 = 1.5f / sqrt(0.5f + (float)n/8192);
Код:
float f4[4096];
for (int n = 0; n < 4096; n++) f4 = 0.5f / sqrt((0.5f + (float)n/8192)*(0.5f + (float)n/8192)*(0.5f + (float)n/8192));
Ну и массивы f1 и f3 можно, КМК, объединить в один.
И точно также массивы f2 и f4 можно, КМК, тоже объединить в один.