1.
Возьмем

-мерное вещественное евклидово пространство

, произвольный базис которого состоит из векторов

.
(То, что у половины этих векторов в обозначении стоит буква

, не должно сбивать нас с толку, пока что это вовсе не значит, что они имеют в себе что-то "комплексное". Это просто обозначение, которое в дальнейшем окажется удобным.)
В пространстве

имеется

подпространств

, каждое из которых имеет базис, состоящий из двух векторов

.
Назовем подпространства

базисными плоскостями пространства

.
Возьмем вектор

,

,
где

его координаты по базису

.
Вектор

можно разложить в сумму

векторов

, каждый из которых принадлежит соответствующей базисной плоскости

:

, - поскольку

является прямой суммой своих подпространств

.
Назовем векторы

составляющими вектора

.
Назовем аргументом вектора

угол между

и базисным вектором

.
(Аргумент вектора

, так же, как и его модуль, можно найти, зная его вещественные координаты по базисным векторам

).
Определим произведение вектора

на комплексное число

следующим образом.
Будем считать результатом перемножения

на

вектор

, модуль которого равен произведению модулей

и

, а аргумент равен сумме их аргументов.
(Для этого пространство

должно быть евклидовым, то есть таким, в котором определены длины векторов и углы между ними).
Каждую составляющую

вектора

можно представить в виде произведения базисного вектора

и комплексного числа

, причем аргумент вектора

равен аргументу комплексного числа

(если вектор

единичный, то и модуль

равен модулю

).
Таким образом,

, где

комплексные числа.
(Пока что мы определили умножение вектора вещественного пространства на комплексное число только для вектора, находящегося в базисной плоскости, но при надлежащем выборе базиса любой вектор пространства может оказаться в базисной плоскости. К тому же немного ниже будет показано, как умножить произвольный вектор пространства - то есть не обязательно находящийся в базисной плоскости, - на комплексное число.)
Теперь, после введения операции умножения векторов на комплексные числа, назовем пространство

комплексным и обозначим его

.
[С момента определения аргумента и модуля составляющей

вектора

мы можем смотреть на них (на аргумент и модуль) как на ее комплексную координату (одна комплексная координата включает в себя и модуль, и аргумент) и на пространство

как на комплексное пространство

.]
Базисом пространства

являются векторы

, то есть его базисная размерность равна

, при том, что осевая размерность (число осей, в которых находятся векторы

) равна

.
При этом векторы

перестали быть базисными.
Таким образом, мы осуществили комплексификацию вещественного пространства

, правда, сделали это не так, как это обычно делается.
Для того, чтобы перейти от комплексных координат

вектора

к его вещественным координатам

надо перевести комплексные координаты каждой составляющей

в вещественные. Для этого достаточно вернуться к представлению, что каждый вектор

находится в вещественном двухмерном пространстве

(подпространстве вещественного пространства

) с базисными векторами

:

, - и, зная его модуль и аргумент (угол относительно вектора

), а также угол между векторами

и их модули, найти его координаты

по векторам

.
При таком представлении у пространства

снова становится

базисных векторов - это все векторы

, - то есть базисная размерность пространства

снова становится

, - само оно снова становится вещественным, и его можно обозначить

, чтобы подчеркнуть, что его векторы умножаются на вещественные числа.
(Осевая и базисная размерность вещественного пространства равны.)
Таким образом,

,
где

вещественные координаты вектора

.
То есть мы произвели овеществление комплексного пространства

.
Чтобы умножить вектор

на комплексное число

(так же, как и в случае умножения его на вещественное число), надо умножить на это число каждую из составляющих

вектора

и полученные произведения сложить:

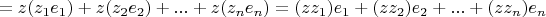
что равносильно (так же, как и при умножении вектора

на вещественное число) умножению на это число (на

) каждой координаты вектора

.
2.
Умножение вектора, лежащего в базисной плоскости

, на комплексное число можно определить в любой форме (не обязательно в геометрической, как мы это сделали).
Независимо от формы, на этот вектор следует смотреть как на комплексное число, которое умножается на другое комплексное число. На ось, в которой лежит базисный вектор

, следует смотреть как на вещественную ось плоскости комплексных чисел, при этом ось, в которой лежит базисный вектор

, не обязана совпадать с мнимой осью.
3.
Назовем линейное пространство, в котором не определены длины векторов и углы между векторами,
просто линейным пространством.
Пусть
 просто линейное
просто линейное вещественное пространство размерности

,

евклидово вещественное пространство той же размерности. Поставим во взаимно-однозначное соответствие каждому вектору

пространства

вектор

пространства

.
Пусть векторы

, векторы

.
Определим произведение вектора

на комплексное число z по формуле
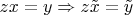
.
Таким образом получаем комплексное
просто линейное пространство

, в котором каждой паре "вектор, комплексное число" ставится в соответствие вектор того же пространства.
Если я ошибаюсь, пусть меня поправят.