Прежде всего - средние в критерии Уилкоксона вообще не используются. То есть в каком смысле автор употребил "в среднем" неясно, похоже, вообще "в бытовом".
По определению функции распределения - если
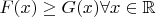
, то для каждого x вероятность, что случайная величина с распределением F(x) будет меньше x,
выше не ниже вероятности того, что случайная величина с распределением G(x) будет меньше x. Возможно, имелось в виду именно это.
Что до средних в смысле матожиданий - можно записать

, записать матожидания обеих величин, выразить разность через интеграл
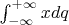
, проинтегрировать по частям

и аккуратно показать, что первое слагаемое это

. Но как аккуратно показать, что при стремлении к бесконечности q(x) убывает быстрее, чем

- не знаю.