а две 1-формы имеют

координат, получается с

не выполняется. Но выше пример для

.
На самом деле, произведение двух 1-форм задается меньшим число параметров, чем

. Это из-за того, что

и
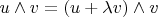
, а также всегда

. Рассмотрим

, где

и

. Применяя соотношение
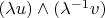
, можно считать, что

. Затем, прибавляя

к

с подходящим коэффициентом, видим, что на самом деле можно считать, что

. Наконец, прибавляя

к

с коэффициентом, видим, что можно ограничиться случаем

. Значит, на самом деле

определяется пятью параметрами.
-- 11.07.2020, 02:52 --(а, вы их через дифференциалы записывали, как в анализе... в общем, разберетесь).
-- 11.07.2020, 02:57 --Но что-то я туплю, не понимаю как в целом сказать, что для

нет соответствия.
Чтоб это нормально сказать, надо знать, что такое "размерность многообразия", аккуратно. Вы, возможно, и не знаете пока.
Проще доказать непосредственно. Только надо иметь в виду, что рассуждение выше в некоторых специальных случаях неприменимо (надо, чтоб в исходном произведении было

).