Топология произведения и непрерывность

[gasel1]

Решаю задачу 1.19(б) из Львовского "Лекции по математическому анализу".

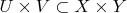
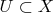
Пусть $X$ и $Y$ - топологические пространства, $X \times Y$ - их декартово произведение. В пункте а) просят показать, что семейство подмножеств $U \times V \subset X \times Y$, где $U \subset X$ и $V \subset Y$ - открыты, образует базу некоторой топологии на $X \times Y$ и что проекции $X \times Y$ на оба сомножителя непрерывны относительно этой топологии. По определению оба утверждения можно доказать.

Но есть еще пункт б). Покажите, что топология произведения на $X \times Y$ является наименее тонкой топологией, относительно которой обе проекции непрерывны. (Если на одном множестве заданы две топологии, то говорят, что первая из них более тонкая, чем вторая, если всякое множество, открытое во второй топологии, открыто и в первой.)

Мне представляется, утверждение пункта не верно. Возьмем тривиальную топологию на $X \times Y$: $\{ \emptyset, X \times Y \}$. Определение непрерывности тривиально выполнено, и эта топология грубее, чем топология произведения. В чем я не прав?

[ИСН]

Э нет, где же оно выполнено? Прообраз любого открытого подмножества должен быть открыт, а у Вас что?