Электрическое поле в диэлектрике

[Solaris86]

Учебник Савельева
Фрагмент 1

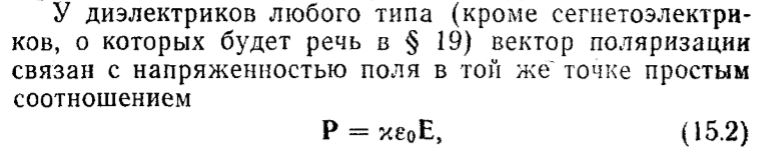
Тут под $\mathbf E$ понимается результирующее поле в диэлектрике как результат сложения векторов внешнего поля, вызвавшего поляризацию диэлектрика, и внутреннего поля в диэлектрике, возникшего в результате поляризации и направленного против внешнего поля.
Фрагмент 2

Тут уже даются конкретные обозначения: $\mathbf E$, как и во фрагменте 1, это результирующее поле в диэлектрике, $\mathbf {E_0}$ - поле свободных зарядов (именно к этой величине дальше будут вопросы), $\mathbf {E'}$ - поле связанных зарядов диэлектрика, возникших в результате поляризации диэлектрика. Фраза "Поляризация диэлектрика обусловлена действием суммарного поля 16.1" вообще не ясна: все поля в формуле 16.1 - это поля внутри диэлектрика, а поляризация, как известно, обусловлена внешним полем, в которое помещён диэлектрик... Как это понимать вообще?
Фрагмент 3

Тут речь идёт о сумме потоков $\Phi_{\mathbf E} = \Phi_{\mathbf E_0} + \Phi_{\mathbf E'} = \frac{1}{\varepsilon_0}(\Sigma q + \Sigma q')$
В данном случае под свободными зарядами, создающими $E_0$, понимаются свободные заряды диэлектрика, в противном случае, если бы речь шла о свободных зарядах вне диэлектрика, то по теореме Гаусса, их поток через замкнутую поверхность диэлектрика равен 0.
Фрагмент 4

Здесь используется уже в скалярном виде формула $E = E_0 - E'$, причём под $E_0$ понимаются свободные заряды вне диэлектрика - свободные заряды проводника (заряженные пластины конденсатора).

Теперь к вопросам:
1. Как может быть в одних и тех же формулах, что $E_0$ - то поле свободных зарядов внутри диэлектрика в формуле 16.1 (соответственно, поток этого поля через замкнутую поверхность диэлектрика отличен от нуля), то поле свободных зарядов вне диэлектрика в формуле 16.17 (соответственно, поток этого поля через замкнутую поверхность диэлектрика отличен от нуля)?
2. Тема свободных зарядов в диэлектрике как-то вообще особо не освещается в учебниках, поэтому не ясно, что же это такое (кроме того, что они в отличие от связанных зарядов могут покидать пределы атома или молекулы и переходить на другие тела). Если под переходом на другие тела имеется в виду электризация типа при натирании шёлком стекла (электроны уходят со стекла на шёлк, оно заряжается положительно и шёлк отрицательно), то тогда не ясно, а как же быть с проводимостью электрического тока, ведь все диэлектрики проводят электрический ток в той или иной степени, и этот ток тоже должны проводить свободные заряды?.. Иногда просто пишут, что в диэлектриках вообще нет свободных зарядов. В общем, какая-то противоречивая тема свободных зарядов в диэлектрике.
3. Самое непонятное: учебнике все рассуждения все рассуждения ведутся при оговаривании, что диэлектрик имеет суммарный нулевой заряд и нулевую поляризацию в отсутствии внешнего поля. Когда подаём внешнее поле, то возникает поляризация, но в расчётах внешнее поле не учитываем (только в формуле 16.11), так как его поток через замкнутую поверхность диэлектрика равен 0. Тогда встаёт вопрос о формуле $\mathbf E =\mathbf {E_0} + \mathbf {E'}$ 16.1, где под $\mathbf {E_0}$ понимается поле свободных зарядов внутри диэлектрика. Во-первых, этих свободных зарядов много меньше, чем связанных зарядов, поэтому величина $E_0$ ничтожно мала по сравнению с $E'$, ей вообще можно пренебречь, по идее. Во-вторых, совершенно нигде не написано, где находятся эти свободные заряды в диэлектрике: если они могут свободно перемещаться, они также должны вместе со вязанными оказаться у поверхностного слоя диэлектрика, но тогда совершенно абсурдно выглядит величина объёмной плотности свободных зарядов, потому что они все у поверхности, а а объёме их нет. Если же это почти свободные заряды (то есть они не могут свободно как свободные заряды в проводнике оказаться в любой точке тела, но они могут перемещаться за пределы атома или молекулы в отличие от связанных зарядов), тогда объёмная плотность свободных зарядов вновь обретает смысл, но становится неясным, как они создают поляризацию (а ведь поляризацию, по условию, создают именно свободные заряды)...
4. Вишенка на торте - фрагмент 5

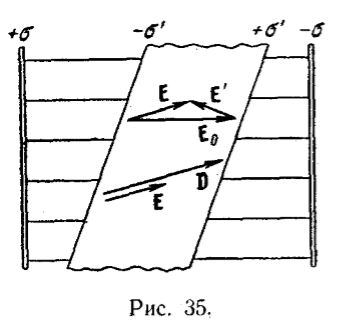
Если по определению $\mathbf D$ определяется только свободными зарядами внутри диэлектрика, а $\mathbf {E'}$ связанными зарядами внутри диэлектрика, то по чему на картинке $|\mathbf D| > |\mathbf {E'}|$, если свободных зарядов в диэлектрике гораздо меньше, чем связанных. Если предположить, что $\mathbf D$ в данном случае обусловлен свободными зарядами вне диэлектрика (например, свободными зарядами пластин конденсатора), тогда возникает проблема с тем, что поток этого вектора через замкнутую поверхность диэлектрика равен нулю и формулы 16.5 и 16.6 фрагмента 6 оказываются неверны:


Помогите разобраться в данном вопросе.

[DimaM]

Solaris86 в сообщении #1473015 писал(а):

все поля в формуле 16.1 - это поля внутри диэлектрика, а поляризация, как известно, обусловлена внешним полем, в которое помещён диэлектрик...

Не нужно употреблять слова, смысл которых не слишком ясен ("обусловлена").
Поляризация в линейных диэлектриках пропорциональна полю внутри диэлектрика. Точка. Как это поле наведено - совсем другой вопрос, слабо связанный с этим.

Solaris86 в сообщении #1473015 писал(а):

В данном случае под свободными зарядами, создающими $E_0$, понимаются свободные заряды диэлектрика, в противном случае, если бы речь шла о свободных зарядах вне диэлектрика, то по теореме Гаусса, их поток через замкнутую поверхность диэлектрика равен 0.

Насколько я понимаю, нет такого разделения ("внутри", "вне"). Берутся все свободные заряды, попавшие внутрь замкнутой поверхности.

[EUgeneUS]

Solaris86
Мне в своё время помогла следующая визуализация:

1. Есть заряды. В проводнике они могут перемещаться под действием электрического поля. Их можно снять "стеклянной палочкой" и "посадить" на поверхность диэлектрика. И даже исхитриться и "посадить" внутрь диэлектрика...

2. И есть диполи. Вот из них и состоит диэлектрик.
i. Диполь нельзя разорвать на два заряда.
ii. Диполь не перемещается внутри диэлектрика, "прибит гвоздями".
iii. Дипольный момент каждого диполя пропорционален внешнему относительно диполя электрическому полю, в точке, где он находится.

3. Поместили диэлектрик в электрическое поле и смотрим, что получается.
а) дипольный момент каждого диполя стал не ноль. Они как-то упорядочились, и создают некое суммарное электрическое поле.
б) по принципу суперпозиции, поле внутри диэлектрика есть сумма внешнего (уже относительно всего диэлектрика), поля зарядов в диэлектрике, буде таковые окажутся, и поля, которое создалось из-за того, что дипольные моменты возникли и-или упорядочились - поле возникшее из-за поляризации диэлектрика.

4. Теперь поместим незаряженную пластину диэлектрика в плоский конденсатор. Внешнее поле однородно, значит и поле, созданное из-за поляризации тоже будет однородным. Тогда можно сказать, что оно создается зарядами, которые находятся на поверхности диэлектрика. И действительно, если разрисовать диполи внутри диэлектрика, окажется, что поля от внутренних диполей компенсируются, а поле создается только диполями на поверхности.

Нужно, помнить, что как любая визуализация, эта имеет свои минусы и ограничения.

[Solaris86]

Вот фрагмент из учебника Трофимовой

DimaM в сообщении #1473019 писал(а):

Насколько я понимаю, нет такого разделения ("внутри", "вне"). Берутся все свободные заряды, попавшие внутрь замкнутой поверхности.

Тогда получается, что есть два вида свободных зарядов:
1) свободные заряды вне диэлектрика (например, пластины конденсатора); речь везде идёт именно об эти свободных зарядах, верно?
2) свободные заряды внутри диэлектрика; этими зарядами пренебрегаем, считая их равными 0; при их наличии возникает неоднородность электрического поля в диэлектрике, о которой пишет Савельев:

Так?

[DimaM]

Solaris86 в сообщении #1473030 писал(а):

Тогда получается, что есть два вида свободных зарядов:
1) свободные заряды вне диэлектрика (например, пластины конденсатора); речь везде идёт именно об эти свободных зарядах, верно?
2) свободные заряды внутри диэлектрика; этими зарядами пренебрегаем, считая их равными 0; при их наличии возникает неоднородность электрического поля в диэлектрике, о которой пишет Савельев:

По моему мнению эти "два вида" ничем друг от друга не отличаются.
Например, возьмем однородный диэлектрический шар и всунем в центр точечный заряд $q$. А во втором таком же шаре сделаем небольшую концентрическую полость и поместим заряд $q$ в ее центр. Поле в диэлектрике, окружающем полость, будет ровно таким же, как и поле в соответствующих местах первого шара.
Более того, вакуум (воздух, гелий, и т.п.) разумно считать диэлектриком с проницаемостью единица, и тогда никаких свободных зарядов "вне диэлектрика" не будет по определению .

[Solaris86]

EUgeneUS
Ваша визуализация мне ясна.
Что вы скажете про свободные заряды именно в диэлектрике и формулы 16.4, 16.5 и 16.6.?
$\Phi_\mathfr D = \Sigma q = \Sigma q_\text{диэл.} + \Sigma q_\text{обкл. конд.}$, то есть сумма свободных зарядов в диэлектрике и свободных зарядов в конденсаторе.
У Савельева написано: "Если свободные заряды распределены внутри замкнутой поверхности непрерывно с объёмной плотностью $\rho$, тогда формула $\Phi_\mathfr D = \Sigma q$ видоизменяется следующим образом:
$\Phi_\mathfr D = \int\limits_{V} \rho dV$
Как могут свободные заряды в присутствии электрического поля РАВНОМЕРНО распределяться в объёме:
1) свободные заряды диэлектрика начнут перемещаться к поверхности диэлектрика (я писал выше, что нигде не указано, на какое расстояние свободные заряды диэлектрика могут отдаляться от атома или молекулы, из которых появились); если свободные заряды диэлектрика дойдут до поверхности, то они должны создать поле, сонаправленное с полем связанных зарядов, то есть ещё больше ослабить внешнее поле в диэлектрике, созданное свободными зарядами обкладок конденсатора;
2) свободные заряды обкладок конденсатора не могут покидать конденсатор и находятся по сути на границах замкнутой поверхности, в объёме (в нашем случае в диэлектрике, находящемся между этими пластинами) их точно нет.
Отсюда напрашивается вывод, что формула $\Phi_\mathfr D = \int\limits_{V} \rho dV$ про объёмную плотность свободных зарядов диэлектрика применима ТОЛЬКО в отсутствии внешнего электрического поля, то есть в отсутствии поляризации, в противном случае никакого равномерного распределения в объёме быть не может...
Так?

-- 09.07.2020, 12:03 --

DimaM в сообщении #1473033 писал(а):

По моему мнению эти "два вида" ничем друг от друга не отличаются.
Например, возьмем однородный диэлектрический шар и всунем в центр точечный заряд $q$. А во втором таком же шаре сделаем небольшую концентрическую полость и поместим заряд $q$ в ее центр. Поле в диэлектрике, окружающем полость, будет ровно таким же, как и поле в соответствующих местах первого шара.
Более того, вакуум (воздух, гелий, и т.п.) разумно считать диэлектриком с проницаемостью единица, и тогда никаких свободных зарядов "вне диэлектрика" не будет по определению .

Тогда также прошу ознакомиться с последним моим постом (адресованным EUgeneUS) про объёмную плотность свободных зарядов.

[EUgeneUS]

Solaris86 в сообщении #1473037 писал(а):

Как могут свободные заряды в присутствии электрического поля РАВНОМЕРНО распределяться в объёме:

Видимо, вот тут и "порылась собака". В трактовке слов "свободные заряды"

Рассматривайте два типа зарядов:
1. Заряды, которые составляют диполи, о которых я писал выше. Считайте, что диполи разорвать нельзя. Вот их и называют "связанными зарядами". Хотя диполи разорвать нельзя, и они не перемещаются по диэлектрику, они могут формировать поверхностную плотность заряда за счет того, что они упорядочены.

2. Заряды "сами по себе", не связанные в диполи. Их можно поместить куда угодно, хоть вне диэлектрика, хоть на поверхность диэлектрика, хоть внутрь диэлектрика. Вот их принято называть "свободными". Но слово "свободные" совсем не означает, что эти заряды могут перемещаться в диэлектрике, аки в проводнике. Куда поместили в диэлектрик, там и они и остаются, диэлектрик же, ток не проводит.

[Solaris86]

EUgeneUS в сообщении #1473038 писал(а):

Куда поместили в диэлектрик, там и они и остаются, диэлектрик же, ток не проводит.

Я правильно понимаю, что мы в данной ситуации ПОЛНОСТЬЮ пренебрегаем электропроводностью диэлектриков и считаем её равной нулю?

[EUgeneUS]

Solaris86
Да.
В задачах электростатики, если есть хоть какая-то электропроводность, то такой материал никак не отличается от проводника.

[Solaris86]

Понятно. Благодарю за разъяснения!