"Неполное" математическое ожидание?

[Divergence]

Введение:
Рассмотрим случайную величину $X$ распределенную на положительной полуоси с плотностью распределения $f_X(x)$.

$$\int^{\infty}_0 f_X(x) dx=1.$$

Математическое ожидание случайно величины $g(X)$:

$$E[g(X)]=\int^{\infty}_0 f_X(x) g(x) dx .$$

Функция распределения случайной величины $X$:

$$F_X(t)=\int^{t}_0 f_X(x) dx.$$

Функция распределения можно интерпретировать как вероятность попадания случайной величины в интервал $[0,t)$.

Вопрос:
Подскажите как можно интерпретировать следующее выражение (функцию):

$$G_{g(X)}(t)=\int^{t}_0 f_X(x) g(x) dx,$$

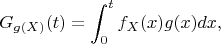
которая совпадает с математическим ожиданием при $t \to \infty$

$$ \lim_{t \to \infty} G_{g(X)}(t) = E[g(X)],$$

а при $g(X)=1$ совпадает с функцией распределения

$$G_{1}(t)=F_X(t).$$

Это что-то типа "математическое ожидание для случайной величины $g(X)$ при попадании случайно величины $X$ в интервал $[0,t)$."

Подскажите какую-нибудь ссылку (на русском или английском), где такая величина (функция) обсуждается и/или используется.

[alisa-lebovski]

Это называется усеченными (или урезанными) моментами, truncated moments.

[Markiyan Hirnyk]

alisa-lebovski Вас не затруднит дать ссылку, точно и полно указав координаты (не нашел такой формулы в Гугле и здесь)? Буду признателен.

[Divergence]

alisa-lebovski спасибо за подсказку.
Однако это "усеченными момент", "truncated moments" - это несколько другое.
Это момент по усеченному распределению, то есть интегрирование с усеченной плотностью распределения.
Эта плотность уже другая - она нормирована на усеченный интервал.

В моем случае, усеченная плотность распределения:

$$ f_{X,t}(x)= \frac{f_X(x)}{F_X(t)},$$

где $F_X(t)$ - функция распределения.
Усеченное математическое ожидание:

$$E[g(X), x<t]=\int^{t}_0 f_{X,t}(x) g(x) dx .$$

Cледовательно,

$$G_{g(X)}(t)=\int^{t}_0 f_X(x) g(x) dx = F_X(t) E[g(X), x<t] .$$

В силу этого, $G_{g(X)}(t)$ - это произведение функции распределения и усеченного математического ожидания.
Это правильно, или нет?

[Евгений Машеров]

Где используется - в финансовой математике. Это цена опциона. Вернее, матожидание выплат по опциону.

[DeBill]

Divergence в сообщении #1472832 писал(а):

Это правильно, или нет?

Да.

[alisa-lebovski]

Markiyan Hirnyk в сообщении #1472805 писал(а):

alisa-lebovski Вас не затруднит дать ссылку, точно и полно указав координаты (не нашел такой формулы в Гугле и здесь)? Буду признателен.

В упомянутом мной смысле словосочетание "урезанные моменты" встречается в русскоязычной литературе, например, в статье
http://www.mathnet.ru/php/archive.phtml ... n_lang=rus

Возможно, в англоязычной это не так. А в словосочетании "truncated moment problem" слово "truncated" относится к "problem", а не "moment" (урезанная проблема моментов).