Нашел в другой книге: там опечатка надо
![$$F(z)=\ln\left[\sqrt{\frac{\ln f(z)}{2\pi i}}-\sqrt{\frac{\ln f(z)}{2\pi i}-1}\right]$$ $$F(z)=\ln\left[\sqrt{\frac{\ln f(z)}{2\pi i}}-\sqrt{\frac{\ln f(z)}{2\pi i}-1}\right]$$](https://dxdy-02.korotkov.co.uk/f/d/6/3/d63c81efcd9c1ff020f7fe153534707a82.png)
Да, это понятно, кроме того, согласуется с формулой для обратной функции из книжки
TelmanStud.
Null
Slav-27
вроде более менее разобрался. Спасибо!
Мне за то, что я там наговорил, по-хорошему надо в дыню, а не спасибо. На всякий случай напишу всё подробно -- вы уже разобрались, но всё-таки.
Напоминание теории:
(Оффтоп)
Канонический аналитический элемент в точке

-- это комплексный степенной ряд

с ненулевым радиусом сходимости.
Это по существу то же самое, что росток голоморфной функции в точке  .
.
Пусть

-- область.
Аналитическая функция на

(в смысле Вейерштрасса -- то есть, вообще говоря, многозначная) -- это максимальное по включению множество канонических аналитических элементов с центрами где-то в

, каждый из которых может быть получен из любого другого аналитическим продолжением вдоль какого-нибудь непрерывного пути, лежащего в

.
Иначе говоря, аналитическая функция -- это связная компонента пучка ростков голоморфных функций на  .
.
Каждый канонический аналитический элемент с центром в

задаёт аналитическую функцию на

-- множество всех канонических аналитических элементов, которые можно получить из него аналитическим продолжением вдоль непрерывных путей, лежащих в

. И обратно, любая аналитическая функция получается таким образом из любого своего элемента.
Теорема Пуанкаре -- Вольтерры гласит, что у аналитической функции в каждой точке не более чем счётное количество элементов. Если у

в каждой точке

ровно один элемент, то она называется голоморфной на

(это согласуется с обычным определением голоморфной функции).
Теорема о монодромии говорит, что если область

односвязна, то любая аналитическая функция на

, имеющая в каждой точке

хотя бы один элемент, голоморфна на

.
Пусть

и

аналитические функции на

. Их сумма

порождается всевозможными

, где

и

-- элементы соответственно

и

с одним и тем же центром; аналогочно определяется произведение

. Композиция

порождается всевозможными

, где

-- элемент

в некоторой точке

, а

-- элемент

в точке

.

не обязательно аналитические функции на

: они, вообще говоря, распадаются на несколько аналитических функций (но, по вышесказанному, не более чем на счётное число).
Надо отметить, что формулы вроде

неоднозначны. Можно понимать это "в широком смысле", то есть как сумму

2 аналитических функций

(которая распадается на 2 аналитические функции:

и

). А можно "в узком смысле": как композицию

функций

и
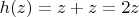
(которая состоит из 1 аналитической функции

). Обычно такие формулы понимают "в наиболее узком возможном смысле", то есть если в формуле несколько раз встречается, например,

, то считают, что элементы квадратного корня во всех этих вхождениях должны быть одинаковые.
Теперь докажем следующее:
Пусть

-- голоморфная функция на открытом круге

радиуса 1 с центром 0, не принимающая значений

и

. Тогда любая из аналитических функций, на которые распадается

, голоморфна на

. (Формула понимается "в узком смысле": два элемента

выбираются каждый раз одинаково. Таким образом, выбор элементов здесь происходит четырежды: у внутреннего логарифма, у каждого из 2 квадратных корней и у внешнего логарифма.)
Так как круг односвязен, то по теореме о монодромии достаточно доказать, что при любом выборе элементов соответствующая аналитическая функция определена (т. е. имеет элемент) в каждой точке круга. Сначала разберёмся с

. Логарифм определён везде, кроме 0; так как

, то

определён в каждой точке круга, и, по теореме о монодромии, любой выбор элемента логарифма даёт голоморфную функцию на

. Квадратный корень тоже определён везде, кроме 0, а

, так как

. Итак, любой выбор элементов внутреннего логарифма и корней приводит к голоморфной функции на

; осталось проверить, что она нигде не обращается в 0. Пусть

(здесь имеются ввиду не сами аналитические функции, а какие-то фиксированные элементы; то есть это равенство (сходящихся) формальных степенных рядов с центром в некоторой фиксированной точке

). Тогда для этих элементов

, откуда
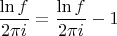
, что приводит к противоречию.
Замечания.
- Мы не говорим, что
 будет состоять ровно из одной голоморфной функции. На самом деле это неверно: к любой из них можно прибавить
будет состоять ровно из одной голоморфной функции. На самом деле это неверно: к любой из них можно прибавить  (
( целое), и получится другая такая голоморфная функция.
целое), и получится другая такая голоморфная функция.
- То, что любые 2 из них отличаются на константу, тоже неверно: можно взять любую из них и измененить знак у выбираемого элемента любого из корней -- полученная голоморфная функция будет отличаться от прежней более чем на константу, если только
 непостоянна.
непостоянна.
- Если понимать формулу "в широком смысле", то есть допустить различный выбор элементов для двух
 , то утверждение остаётся верным (но при некоторых выборах элементов под внешним логарифмом будет получаться тождественный ноль, не дающий никакой аналитической функции).
, то утверждение остаётся верным (но при некоторых выборах элементов под внешним логарифмом будет получаться тождественный ноль, не дающий никакой аналитической функции).
- Пусть
 голоморфная функция на односвязной области. Мы использовали тот факт, что если
голоморфная функция на односвязной области. Мы использовали тот факт, что если  не обращается в 0, то любая из аналитических функций, на которые распадается
не обращается в 0, то любая из аналитических функций, на которые распадается  , голоморфна. Верно и обратное: если хотя бы одна из аналитических функций, на которые распадается
, голоморфна. Верно и обратное: если хотя бы одна из аналитических функций, на которые распадается  , голоморфна, то
, голоморфна, то  не обращается в
не обращается в  . Действительно, в таком случае
. Действительно, в таком случае  есть экспонента голоморфной функции, а экспонента никогда не обращается в
есть экспонента голоморфной функции, а экспонента никогда не обращается в  .
.
- Вообще говоря, неверно, что любой элемент
 есть композиция некоторого элемента
есть композиция некоторого элемента  с некоторым элементом
с некоторым элементом  : может оказаться, что аналитическое продолжение какого-нибудь элемента такого вида даёт элемент, не имеющий такого вида. Пример:
: может оказаться, что аналитическое продолжение какого-нибудь элемента такого вида даёт элемент, не имеющий такого вида. Пример:  ,
,  . Композиция
. Композиция  , но её элемент в
, но её элемент в  не имеет такого вида, потому что у
не имеет такого вида, потому что у  вообще нет ни одного элемента в нуле. Мы выше рассматривали элементы только такого вида, пользуясь теоремой о монодромии: если есть элемент такого вида, то никаких других в этой точке быть уже не может.
вообще нет ни одного элемента в нуле. Мы выше рассматривали элементы только такого вида, пользуясь теоремой о монодромии: если есть элемент такого вида, то никаких других в этой точке быть уже не может.
Исследуем заодно и формулу с опечаткой

.
(Оффтоп)
Будем понимать её "в узком смысле", то есть как
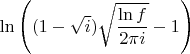
. (Так как

постоянная функция, то эта формула сразу распадается на 2 формулы

и

.)
Разумеется, тут уже неверно, что для любой

любая из аналитических функций, которую эта формула задаёт, обязательно голоморфна. Чтобы в этом убедиться, достаточно придумать непостоянную голоморфную

на

, которая не принимает значений

и

, но равна в некоторой точке, скажем,

; существование такой функции сразу следует, например, из теоремы Римана (о том, что любая односвязная область в

, отличная от всей

, биголоморфна единичному кругу).
Можно сказать и больше: существует такая голоморфная

на

(не принимающая значений 0 и 1), что
ни одна из аналитических функций, задаваемых вышеприведённой формулой, не является голоморфной!
А именно, выкинем из

дерево

(связный граф без циклов), проходящее через все квадратные корни из целых чисел, но не проходящее через числа вида

, где

целые. (Думаю, что подойдёт
![$\Gamma:=\{\sqrt k e^{i\varphi}| k\in\mathbb N, 0\leqslant\varphi\leqslant\frac{3\pi}2\}\cup (-\infty,0]$ $\Gamma:=\{\sqrt k e^{i\varphi}| k\in\mathbb N, 0\leqslant\varphi\leqslant\frac{3\pi}2\}\cup (-\infty,0]$](https://dxdy-03.korotkov.co.uk/f/a/1/e/a1ecda20a8c8fe0eedfbbe741fe8ef3682.png)
.) Получится односвязная область

; по теореме Римана найдётся (даже би-) голоморфная функция

, отображающая единичный круг на эту область. Тогда голоморфная функция

обладает требуемым свойством.
Действительно, во-первых,

не обращается в 0 (так как она экспонента голоморфной функции) и в 1 (так как область значений

не содержит квадратных корней из целых чисел). Зафиксируем выбор элемента корня и логарифма

, приводящий к функции

: тогда голоморфная функция под внешним логарифмом принимает значение

(потому что

принимает каждое из 2 значений

по построению

). Любой другой выбор элементов корня и логарифма даёт элемент вида

; здесь

обозначает элемент, который мы зафиксировали раньше,

-- любой из 2 возможных элементов корня, а

-- какое-то целое число. Докажем, что порождаемая этим элементом голоморфная функция принимает каждое из 4 значений

. Во-первых, квадрат этого элемента

порождает

, которая принимает значения

, так как

принимает все значения

(опять-таки по построению

). Осталось проверить, что если

и при этом

, то и

для любого (из двух, отличающихся только знаком) выбора голоморфной функции

. Это следует из того, что на области

одна из двух голоморфных функций
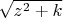
отображает каждый из 4 открытых квадрантов в этот же самый открытый квадрант (а другая, соответственно, переставляет квадранты отражением относительно 0).