Добрый день всем!
Задача формулируется так:
Пусть ![$L=[-1,-9]\cup [-9,-9+i]\cup[-9+i,\infty+i)$ $L=[-1,-9]\cup [-9,-9+i]\cup[-9+i,\infty+i)$](https://dxdy-01.korotkov.co.uk/f/c/f/2/cf22cedd3ce071ad4e217ec334ebb9ae82.png) и пусть
и пусть  . Пусть
. Пусть  - голоморфная ветвь
- голоморфная ветвь 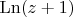 в
в  такая, что
такая, что  . Разложить
. Разложить  в ряд Тейлора с центром в точке
в ряд Тейлора с центром в точке  , определить радиус сходимости полученного ряда и показать, к какой функции сходится этот ряд в своем круге сходимости (указание: обратить внимание на то, что
, определить радиус сходимости полученного ряда и показать, к какой функции сходится этот ряд в своем круге сходимости (указание: обратить внимание на то, что  может пересекать этот круг
может пересекать этот кругОтветить на вопрос о разложении в ряд вроде бы не сложно:

Область сходимости будет

Но вот вопрос, к чему сходится этот ряд в его области сходимости, напоминает мне анекдот
(Оффтоп)
Американцы достали инструкции и чертежи русского сверхсекретного истребителя. Все детали по чертежам сделали, собрали - получился локомотив. Ладно, разобрали, еще раз проверили по чертежам, собрали - опять локомотив. Американцы, ничего не понимая, выкрали русского конструктора:
- Что за ерунда?! Почему вместо истребителя получается локомотив?!
А он им отвечает:
- А вы посмотрите, там на чертежах внизу мелким шрифтом: после сборки обработать напильником
В общем, я что-то не совсем понимаю, почему в области сходимости, даже если она пересекается с каким-то лучом, который мы "выключаем" из области исследования функции, ряд должен сходиться к функции отличной от той, которую мы разложили. Подскажите, в чем тут дело?