пианист,
Padawan, большое спасибо за Ваши ответы. Пока что из того, что есть, они наиболее содержательны. Я же вообще ставлю вопрос более общо: в книгах Эльсгольца и Степанова, о которых я уже упоминал, речь идёт об отыскании общих решений уравнений в частных производных в виде

при этом, делается это (в обоих источниках) при дополнительном условии

о котором я также писал выше. Возникает вопрос (который я уже ставил, но видимо, был не вполне правильно понят некоторыми участниками): не возникает ли от этого предположения потери решений ? Кроме того, именно из-за условия

беря потом частные производные от

мы можем выразить


и так далее. Именно так и делают авторы указанных книг. Но, как мы видели по конкретной задаче, некоторые из подобных функций

для конкретных уравнений могут и не удовлетворять условию
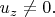
Возникает вопрос и по поводу того, насколько корректным становится отыскание таких функций

, если предполагается одно условие, а результат решения нарушает это условие, и насколько корректным является запись общего решения в соответствующем виде (точнее: не является ли изложение материала из указанных книг некой "вольностью" со стороны авторов ?).