Положим, единичный оператор мы можем сразу вычесть, у него всегда одна и та же матрица. Остаются двойки и тройки. Подкорректировав базис, мы можем сделать из них единицы. Теперь просто меняем порядок векторов в базисе и внезапно
Давайте мы сначала поменяем порядок :) Тогда наши матрицы уже станут сильно похожи: отличается только число на диагонали повыше главной.
Теперь по поводу вычитания единичной матрицы. Получается, что матрицы

и

подобны тогда и только тогда, когда подобны матрицы
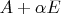
и
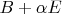
, где
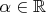
. Это гениально, я с этим согласен, это прямо тянет на отдельную теорему.
Теперь осталось только доказать, что матрицы с тройками на диагонали повыше главной и двойками на той же диагонали подобны. Вы пишете
Подкорректировав базис, мы можем сделать из них единицы
и вот это я не совсем понимаю, как сделать, честно говоря...
-- 30.05.2020, 18:24 --Базисные векторы можно удлинять и укорачивать.
Ну да, то есть, получается, скажем,

. Я укорачиваю

вдвое и получаю там единицу. Далее

, а значит

нужно укоротить в 4 раза... Да, получается!