Ludmila_Еще раз: в задаче требуется показать, что ЕСЛИ матрица коммутирует с любой другой, то она имеет вид

.
Вам предлагается следующий путь доказательства: предположим, что

, тогда можно найти такую матрицу

, что коммутации нет:

.
Отличаться от

можно двумя основными способами (остальное - их комбинации):
1) Матрица отличается от

, тем, что есть ненулевой элемент вне диагонали:
Предположим, что некоторый элемент

,
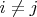
, матрицы

не равен нулю. Придумайте такую матрицу

, что

.
2) Матрица отличается от

, тем, что есть элемент на диагонали, отличный от других на диагонали (вне диагонали все элементы нулевые):
Затем, пусть

, где
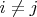
. Придумайте такую матрицу

, что

.