я вот к чему: аксиоматика моноидов и аксиоматика полугрупп могут формулироваться в одном и том же языке. При этом сигнатура одна и та же. Никаких операций (в том числе констант) у нас в распоряжении нет, кроме одной единственной полугрупповой операции. Утверждение
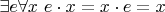
не содержит никаких функциональных символов (в том числе константных), кроме символа

. Всё различие сводится к тому, что для полугрупп это независимое утверждение, а для моноидов — аксиома.
Ну если мы моноид определяем, не внося

в сигнатуру, то печально, конечно. Тогда можно отобразить весь первый моноид в любой идемпотент второго, не являющийся нейтральным, и это действительно всё ломает.
С этим однако нетрудно разобраться, ограничив возможный вид аксиом (никаких

, всё переделать в операции; плюс может что-то ещё потребоваться). Выражаясь категорным языком,

относится к структуре, а отнюдь не к свойствам*, и вполне разумно требование все данные держать в сигнатуре (а свойства требовать аксиомами). Или могут быть ещё подходы.
* Ср. с абелевыми группами и группами — любой морфизм групп будет морфизмом и абелевых групп, если эти группы абелевы; потому кстати вы нигде не найдёте отдельного определения морфизма для специфически абелевых групп, но действительно находите отдельное определение морфизма моноидов.Но тогда можно было бы доопределить ещё несколько операций и отношений и потребовать, чтобы они тоже сохранялись при гомоморфизмах, и этим окончательно добить "определение".
Пока мы просто добавляем в сигнатуру какие-то штуки, не снабжая их аксиомами, это ещё куда ни шло, но если мы будем связывать их со старыми частями, то мы действительно можем добиться аналогичного тому, что выходит при переходе от полугрупп к моноидам — нельзя на полугруппе «определить дополнительно» нейтральный элемент, можно его иметь (и тут сравнение в другую сторону: к любому векторному пространству можно например приделать симметричную невырожденную билинейную форму, несмотря на то что её аксиомы используют и

, и

, чтобы хотя бы выразить билинейность).
другая нульарная (она выделяет особый элемент - единицу)
ТС говорит о (не)хитром определении моноида, позволяемом логикой первого порядка, где операция в сигнатуре только одна, а существование нейтрального элемента — это часть аксиомы, а не утверждение о том, что в сигнатуру входит и символ для него. Тогда действительно неудобно получается (

может вполне переходить в какой-то другой идемпотентный), но с учётом того, что я не видел ни одного человека, который бы что-то делал с моноидами и при этом упорно не вводил константу для

, я бы посчитал такие определения с экзистенциальной аксиомой не очень-то честными и как выше предложил бы их исключить из рассмотрения.
Правда может ещё какой-нибудь казус вылезти (который логики скорее всего уже давно поймали, но другим особо не рассказывали, и про который я может быть даже сам где-то читал, но сейчас забыл), но когда вылезет, тогда и подумаем.