Спасибо за подсказки. Попробую сделать оценки.
Сначала оценим

. Если оценивать грубо, то каждое число в произведении факториала не больше 100, значит
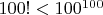
. Но это будет слишком грубо. Можно не столь грубо сделать так. Половина чисел в произведении не более 50, потому

. Можно уточнять оценку далее.
Если самое грубое приближение использовать
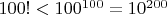
, то цифр в

не более 201.
Если рассмотреть

, то ясно, что раз у

не более

цифры, то сумма этих цифр не более

. Если число не более

, то сумма цифр не более

Значит

не более

, а значит ,

,

....а значит я что-то не так делаю))
-- 26.05.2020, 23:27 --Вот очевидно, что

делится на 9, а вот дальше - не ясно.
Ну дык раз

делится на

, то и сумма цифр

делится на


Кажется это означает, что начиная с некоторого

у нас

. Интуиция мне подсказывает, что сведется это к тому, что мы получим последнее число, которое делится на 9, если сумма цифр будет быстро убывать, а если будет убывать не очень быстро, то некое число, которое делится на 9 будет в ответе, он что-то мне подсказывает, что сумма цифр убывает быстро!