Но идею доказательства вы понимаете? Почему вообще меняется знак определителя, когда две строки поменять местами, если на пальцах, понятно?
Еще момент. Вам понятно, что

для любых
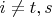
и

и

?
где

.
Только у него

- это те перестановки (все возможные), по которым ведется суммирование, а
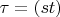
- это осуществленная перестановка строк.
-- 25.05.2020, 23:37 --После исправлений стало совсем непонятно. Исходная и "переставленная" матрица состоят из одинакового набора элементов, а обозначения их элементов стали разными- со штрихами и без них?
Мне кажется, все понятно. В новой матрицы все элементы обозначаются со штрихами, при этом большинство из них равны соответствующим элементам без штрихов, кроме тех, которые находятся в двух "поменяных" строках.