Здравствуйте! Помогите, пожалуйста, разобраться! Есть ли способ проще? Я вижу только в лоб. Неравенство для 8 класса.
Есть неравенство

Можно раскрыть скобки. Получаем

Иными словами

Далее, раскладываем многочлен на множители, получаем

Ну и очевидно, что

, квадрат неотрицательный, неравенство доказано.
Можно еще с другой стороны было зайти. Если

, то
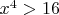
, а значит

.
Если

, то

, а значит

.
Осталось рассмотреть случай

, но вот тут уже не очевидно. Как быть?
Можно, конечно, рассмотреть графический способ, но есть ли варианты проще?