Тогда получается, что эта кривая в комплексной плоскости состоит из трех компонент: двух ветвей гиперболы и единичной окружности, которая их связывает. Так?
Нет, не так. Рассмотрим пока лишь многообразия в действительном пространстве. Множество точек в трехмерном пространстве, обычном, определяемое двумя уравнениями, это что такое ? Не лишним будет спросить: вы курс обычной аналитической геометрии брали ? Или устремились сразу к алгебраической ? Вот это замечание
сли подставить

и

в уравнение кривой, то получим:

, тогда

и

Эти кривые похожи на параболы.
наводит на мысль, что нет...
-- 18.05.2020, 01:56 --Полезно также вообще посмотреть, что собой представляет эта комплексная кривая как двумерное многообразие в четырехмерном действительном пространстве
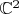
, порисовать разные сечения и т.п.
Я думаю, это не такой уж простой вопрос. Я, во всяком случае, сейчас обозримого ответа на него не вижу. Топологически понятно, что это будет, а вот с других точек зрения --- непонятно.