Метод Фурье для уравнения теплопроводности в кольце

[Juicer]

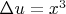
Дано уравнение теплопроводности $\Delta u = x^3$ с областью $1 \leq x^2 + y^2 \leq 4, x \geq 0.$
Условия на границах области: $u'_x|_{x = 0} = 0, u|_{r = 1} = u|_{r = 2} = 0.$
Решается она методом Фурье, в полярных координатах. Вопрос: известно, что круговые области раскладываются в ряд Фурье с коэффициентами, содержащими и косинусы, и синусы. Короче говоря, ряд Фурье нашей функции $u$ будет выглядеть следующим образом:

$$u = \sum_{k = 0}^\infty u_k(r)\cos(k \varphi) + \sum_{k = 1}^\infty v_k(r)\sin(k \varphi).$$

Но вспоминаем, что на границе у нас производная обращается в ноль: $u'_x|_{x = 0} = 0$. Можем ли мы утверждать, что можем разложить лишь по косинусам (подобным образом делается для прямоугольных областей), не включая синусов? Или для чего применить эту производную - не могу понять.
Если бы это было так, то очень удобно получалось: $x^3 = (r \cos \varphi)^3 = 3/4 r^3 \cos \varphi + 1/4 r^3 \cos 3 \varphi$.
Понимаю, что из $u'_x|_{x = 0} = 0$ следует $u'_\varphi = 0$.

[pogulyat_vyshel]

Juicer в сообщении #1463266 писал(а):

Можем ли мы утверждать, что можем разложить лишь по косинусам

ну так подставьте и посмотрите сможете ли вы все краевые условия удовлетворить

[Juicer]

pogulyat_vyshel в сообщении #1463275 писал(а):

ну так подставьте

Получается, если подставить разложение только с $\cos$, у нас производная в ноль обратится, а если же и с $\cos$, и с $\sin$ - нет, ибо $\cos(1) = 1$ и синусы не участвуют в итоговом разложении.
Так?
UPD: Просто от этого зависит, можно ли оставить, как я разложил $x^3$, или нужно ещё этот куб раскладывать в ряд Фурье сам

[Red_Herring]

Такие задачи следует начинать решать не (с фонаря взятого) ряда Фурье, а с разделения переменных (когда в правой части $0$), решения задачи ШтурмаьЛиувилля (по $\varphi$) и нахождения, по каким функциям следует разлагать. В данном очень конкретном случае ответ действительно $\cos(n\varphi)$, но в общем случае это не так.