NormaНечетная непрерывная функция обязана проходить через точку

Чтобы график функции "косинусом" проходил через точку

его нужно сдвинуть влево, например, на
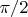
, либо вправо на

. В результате получится то, что советовал уважаемый
DeBill - "косинус станет синусом"