Метод наименьших максимумов

[boris926]

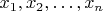
Пусть $x_1, x_2, \ldots, x_n$ - вещественные числа.

Легко получить, что решение задачи (метод наименьших квадратов)

$$ \sum_{k=1}^{n}(x-x_{k})^2 \to \min_{x\in\mathbb{R}} $$

есть среднее арифметическое

$$ x^{\ast} = \frac{1}{n}\sum_{k=1}^{n}x_{k}. $$

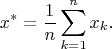
Также известно, что решением задачи (метод наименьших модулей)

$$ \sum_{k=1}^{n}|x-x_{k}| \to \min_{x\in\mathbb{R}} $$

является выборочная медиана набора чисел $x_1, x_2, \ldots, x_n$.

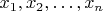
У меня возник вопрос. А что если рассмотреть "метод наименьших максимумов"? Существует ли такой метод? Я имею в виду задачу

$$ \max_{1\leq k\leq n} |x-x_{k}| \to \min_{x\in\mathbb{R}}. $$

Что является решением этой задачи? Я попытался рассуждать так. Без ограничения общности будем считать, что все $%x_{k}$% уже упорядочены по возрастанию, т.е. $x_1\leq x_2\leq \ldots\leq x_n$. Но как двигаться дальше?

[Someone]

boris926 в сообщении #1460563 писал(а):

$$ \max_{1\leq k\leq n} |x-x_{k}| \to \min_{x\in\mathbb{R}}. $$

Что является решением этой задачи? Я попытался рассуждать так. Без ограничения общности будем считать, что все $%x_{k}$% уже упорядочены по возрастанию, т.е. $x_1\leq x_2\leq \ldots\leq x_n$.

$\frac 12(x_1+x_n)$?

[Евгений Машеров]

Чебышевское приближение? (Это в общем случае, для поиска параметра положения уже ответили - середина размаха).