Экспоненциальный интеграл в подынтегральной функции

[alunev]

Добрый день!

Интересует следующий интеграл:

$ \int_a^b{f(t) E_n(\alpha + \beta t)dt}. $

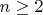
Здесь $E_n(t) = \int_0^1{e^{-\frac{t}{\mu}} \mu^{n-2} d \mu }$, то есть экспоненциальный интеграл порядка $n \geq 2$, без сингулярности в нуле (на случай, если нижний предел совпадает с нулём). Функция $f(t)$ - ограниченная, гладкая на интересующем отрезке (задана дискретно).

Какой метод лучше использовать для вычисления этого интеграла с наименьшими временными затратами (желательно без вычисления экспонент)? Пока что пробовал разбиение по правилу Симпсона и прочие формулы Котеса, но слишком много точек требуется, чтобы получить вменяемую точность (до $128$, это уже много). Подскажите, стоит ли смотреть в сторону метода Гаусса-Лагерра - и если да, то как лучше преобразовать подынтегральную функцию, чтобы наименее время-затратно взять этот интеграл? Пока всё, что видел, приводит к появлению экспоненциальных множителей, которые считать неэффективно на машине. Есть сомнения в том, будет ли это быстрее.

Может, есть какая-то более простая альтернатива?

Спасибо!

[Утундрий]

Переставлять порядок интегрирования пробовали?

[Dan B-Yallay]

alunev в сообщении #1460506 писал(а):

Здесь $E_n(t) = \int_0^1{e^{-\frac{t}{\mu}} \mu^{n-2} d \mu }$,

Не обязуюсь помочь с вычислениями, но мимо пройти не смог: y вас левая часть зависит от $t$ а правая... ?

[alunev]

Dan B-Yallay:
В правой части $t$ - в показателе экспоненты.

Утундрий
Ну, я понимаю, что можно так. Можно представить в виде $\int_0^1{\mu^{n-2} d\mu \int_a^b{e^{-t/\mu} f(t) dt } }$, дальше что делать? Внутренний интеграл по формуле Гаусса-Лагерра (с поправкой на пределы интегрирования), внешний - по методу Гаусса с полиномами Лежандра? Или нужно еще во что-то преобразовать? Если пользовались этими формулами, сколько обычно членов требуется взять в методе Г-Л? Как избежать вычисления функций $L_n(x)$ - брать заранее табулированные величины?

[Dan B-Yallay]

alunev в сообщении #1460514 писал(а):

В правой части $t$ - в показателе экспоненты.

Извиняюсь, сослепу не разглядел, увидел там 1.

[Утундрий]

alunev в сообщении #1460514 писал(а):

Можно представить в виде $\int_0^1{\mu^{n-2} d\mu \int_a^b{e^{-t/\mu} f(t) dt } }$

Точнее

$$\int_0^1{\mu^{n-2} d\mu \int_a^b{e^{-(\alpha + \beta t)/ \mu} f(t) dt } }$$

alunev в сообщении #1460514 писал(а):

дальше что делать? Внутренний интеграл по формуле Гаусса-Лагерра (с поправкой на пределы интегрирования), внешний - по методу Гаусса с полиномами Лежандра? Или нужно еще во что-то преобразовать? Если пользовались этими формулами, сколько обычно членов требуется взять в методе Г-Л? Как избежать вычисления функций $L_n(x)$ - брать заранее табулированные величины?

Ну, так уж далеко я не заходил. Просто подумал, что так может оказаться быстрее. Попробуйте, сравните...

[mihiv]

Если у вас интервал интегрирования разбит на отрезки равной длины $h$, то вычисление экспоненты в точке разбиения можно свести к однократному умножению. Пусть $a_k=e^{-kh}, q=e^{-h}$, тогда $a_{k+1}=a_kq$.

[alunev]

Для тех, кому интересно: решение такого и подобного интегралов, включая случай $n = 1$, подробно разобрано в книге Chandrasekhar, Subrahmanyan. Radiative transfer, параграф 23, стр. 66-67 (Quadrature formulas) по изданию 1960 г. (Dover Books). Книгу можно скачать на либгене.