Так что именно Вы хотите узнать?
Мне хочется понять, как решать легко придумываемый (но тяжело пока что берущийся) интеграл вида
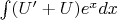
.
Потому что каждый, даже очень страшный на вид интеграл можно построить банальным образом
Да, вы сформулировали то, что я пытался сформулировать!
До сих пор я никогда не мог сам придумывать интегралы, которые при этом не мог бы потом взять. Более того, "хитрые" интегралы (особенно неопределенные, об определенных другой разговор) было "днем с огнем", не так уж просто и найти. Возьмите любой задачник, реально берущихся, но при этом непонятно как, интегралов в них не так уж и много. И тут я в руки получаю способ составлять на первый взгляд неберущиеся, но при этом берущиеся, интегралы, в неограниченных количествах. Можете считать, что я не могу в это поверить, и пытаюсь понять, где общий способ решения.
Уважаемые участники комментируют, что можно использовать алгоритм Риша и в таком духе, и это понятно, его всегда можно использовать :)
К примеру, вы знаете способ составлять берующиеся, но сложные, интегралы from the scratch? Описанный вами способ, мне кажется, не работает. Это надо очень постараться (либо должно сильно повезти), чтобы, продифференцировав какую-то даже большую функцию, получить компактное выражение, чтобы человек, у которого большой опыт интегрирования, прямо почесал голову и сказал, что не знает, что тут делать. У меня так пока не получалось.