Mihayloспасибо, нашел, вот, что получилось:


Я сегодня об этом думал, но забыл, что там не ступенька (sign), а что-то другое. Начал визуализировать прямую - пересечение с плоскостью

, а она работала через раз (иногда перекрывала объекты), теперь ясно почему.
Может, кого-то это ещё заинтересует, поэтому оставлю код и скрины.
from matplotlib import pyplot as plt
import numpy as np
from sklearn.linear_model import SGDClassifier
def lin_log(w, b):
def func(x):
return (0.5 - w[0] * x - b) / w[1]
return func
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 0, 0, 1])
model = SGDClassifier()
model.fit(X, y)
w = model.coef_[0]
b = model.intercept_[0]
x_min, x_max = -2, 2
y_min, y_max = -2, 2
fig, ax = plt.subplots()
linear = lin_log(w, b)
grid_x = np.linspace(-3, 3, 200)
grid_y = linear(grid_x)
ax.plot(grid_x, grid_y)
ax.scatter(X[:, 0], X[:, 1])
ax.grid(which='major',
color='k')
ax.axis([x_min, x_max, y_min, y_max])
plt.show()
 -- 14.04.2020, 02:19 --Mihaylo
-- 14.04.2020, 02:19 --Mihayloтолько сейчас обратил внимание, везде пишут по-разному, то

, то
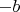
. Я, наверное, что-то не понимаю, но это несколько разные вещи, нет? То есть смещения получаются одинаковые в обоих случаях, но разные по знаку, разве нет?