На отрезке случайным образом выбирают два числа..

[mvb13]

Здраствуйте
Мне очень нужно проверить решение данной задачи. Подскажите пожалуйста правильно ли я ее решил.

Условие:
На отрезке [-2,2] случайным образом выбираются два числа. Найти вероятность того, что наименьшее из них принадлежит отрезку [-1,1].

Ввожу в рассмотрения слдеующие события:
$A=\{ $ наименьшее из 2 чисел принадлежит отрезку $ [-1,1] \}$.
$A_2=\{ a\in[-1,1] \}$
$A_3=\{ a\in [1,2] \}$
$B_2=\{ b\in[-1,1] \}$
$B_3=\{ b\in [1,2] \}$

Событие A состоит из 3 попарно несовместных событий:
$A=A_2B_2+A_2B_3+A_3B_2$

События, несовместны поэтомму из аксиомы следует:
$P(A)=P(A_2B_2)+P(A_2B_3)+P(A_3B_2)$

В тоже время события $A_2B_2, A_2B_3, A_3B_2$ являются независимыми(т.к. числа выбираются случайным образом)

Поэтому из определения независимых событий:
$P(A)=P(A_2)P(B_2)+P(A_2)P(B_3)+P(A_3)P(B_2)$

В этом месте у меня вопрос. У меня в конспекте единственный параграф помогающий определить вероятность (Схема геометрической вероятности). В нем есть определение
$P(A)$ для области на плоскости и формула для $\mathbb{R}^n : P(A)=\frac{mes(A)}{mes(\Omega)}$.

1.Не понятно что обозначается символом $mes$
2.Можно ли применить эту формулу для $n=1$

$P(A)=\frac{2}{4}*\frac{2}{4}+\frac{2}{4}*\frac{1}{4}+\frac{1}{4}*\frac{2}{4}=\frac{1}{2}$

[Brukvalub]

mvb13 в сообщении #144277 писал(а):

Ввожу в рассмотрения слдеующие события:
$A=\{ $ наименьшее из 2 чисел принадлежит отрезку $ [-1,1] \}$.
$A_2=\{ a\in[-1,1] \}$ $A_3=\{ a\in [1,2] \}$ $B_2=\{ b\in[-1,1] \}$ $B_3=\{ b\in [1,2] \}$
Событие A состоит из 3 попарно несовместных событий:
$A=A_2B_2+A_2B_3+A_3B_2$

Случай a=b=1 показывает, что выбранные Вами события совместны.

Добавлено спустя 2 минуты 5 секунд:

mvb13 в сообщении #144277 писал(а):

1.Не понятно что обозначается символом $mes$

Этим символом обозначена мера множества (длина, площадь, объем и т.д., в зависимости от размерности). При $n=1$ это будет длина.

[PAV]

Действительно можно решать так, как Вы делали, а можно с помощью геометрических вероятностей. Нужно рассмотреть в декартовой системе координат на плоскости квадрат $[-2,2]\times[-2,2]$: точка на оси абсцисс соответствует первому выбранному числу, а на оси ординат - второму. Изобразите на этом квадрате геометрическое место точек, при которых выполняется требуемое условие. И ищите вероятность попадания точки в эту фигуру по приведенной Вами формуле.

[mvb13]

С этой задачей разобрался. Спасибо за помощь.

Помогите пожалуйста еще со второй задачей:

На шахматную доску наудачу ставят двух слонов. Какова вероятность , что слоны побьют друг друга?

$A= \{$ Слоны побьют друг друга \} $

Количество вариантов распределить номера клеток для двух слонов равно
$C_{64}^2 = 2016$

Шахматную доску рассматриваю ,как таблицу.
Помещаю первого слона в ячейку [1][1] (номер строки, номер столбца). Для размещения второго слона остается 7 способов. Для первой строки любого столбца существует 7 вариантов. Перемещаю первого слона в положение [2][1] . Здесь существует 7 вариантов размещения второго слона [3][2] , [4][3] , [5][4] , [6][5] , [7][6] , [8][7] и вариант [1][2] . Но этот вариант уже был посчитан, когда первый слон ноходился в этом положении, а второй в позиции первого.(имеет значение только взаимное расположение слонов) Таким образом считаю только ячейки у которых номер строки больше номера строки в которой расположен первый слон.



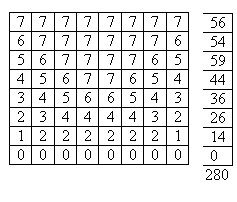
Для каждой клетки определяю количество возможных расположений второго слона(первый слон находится в данной клетке).

1.Правильно ли такое решение?
2. Можно ли в данном случае применить формулы комбинаторики?

$P(A)=\frac {280} {2016}=0.14$

[mvb13]

Помогите пожалуйста . Мне очень срочно нужна эта задача.

[faruk]

У меня такой же ответ получился.

$P=\displaystyle\frac{28}{64}\cdot\frac{7}{63}+\frac{20}{64}\cdot\frac{9}{63}+\frac{12}{64}\cdot\frac{11}{63}+\frac{4}{64}\cdot\frac{13}{63}=\frac{560}{4032}$

[AndriyMarevich]

mvb13 в сообщении #144277 писал(а):

Условие:
На отрезке [-2,2] случайным образом выбираются два числа. Найти вероятность того, что наименьшее из них принадлежит отрезку [-1,1].

Это есть вероятность того, что хоть одно число ринадлежит отрезку [-1;1]
P=1-2/4*2/4=3/4

[PAV]

AndriyMarevich
если уж Вам так по душе поднимать темы двух- и более годичной давности, то уж хотя бы таких очевидных ошибок не пишите. События "наименьшее число принадлежит $[-1,1]$" и "хотя бы одно число принадлежит $[-1,1]$" - это очевидно разные события. Первое является строго подмножеством второго.