Может быть, кто-нибудь знает, почему так происходит?
Пришла мысль, если

производная равна нулю на отрезке, то

производная
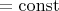
, а значит

производные тоже совпадают у многочлена и функции ну и так далее, получается, что значения этих функций совпадают на отрезке, вроде же верно? И тогда получается, что чем меньше

производная на отрезке, тем больше совпадают многочлен и функция на отрезке
Ну вот, прекрасно, Вы сами догадываетесь уже, что там и почему происходит.
Есть еще такой общий принцип: если в какое-то утверждение или задачу входит натуральный параметр, то для понимания надо сначала смотреть на ситуацию, в которой этот параметр мал (скажем, равен

), обдумать, потом на

смотреть, потом на общее

. (А иногда наоборот, проще понять требуемое для больших

). И вообще надо от более простой ситуации к более сложной переходить постепенно. Скажем, задаться вопросом: что можно сказать про поведение функции, если она непрерывна в точке

? Непрерывна в интервале, содержащем

? Дифференцируема в

? Дифференцируема в интервале, содержащем

? Дифференцируема в этом интервале, причем производная там непрерывна ? Дважды дифферецируема в точке ? Дважды дифференцируема в инервале ? И т.д. И как это отражается на ее приближенных выражениях, типа формулы Тейлора, в окрестности этой точки ?
Можете попробовать доказать в качестве упражнения (в учебниках этого нет), что если

дифференцируема в некотором интервале, содержащем

, и производная в этом интервале лишицева
(Липшицевость)
Функция
 липшицева
липшицева в интервале

, если существует константа

такая, что

для любых

.
то

. Если, читая учебники, Вы самостоятельно решите эту задачу, то поймете, что такое формула Тейлора и с чем её кушают. (Увидев соответствующие понятия, так сказать, "в работе", а не со стороны).