У людей, постоянно решающих подобные задачи, могут быть свои умолчания, которые могут не уловить новички, набредшие на интересную задачу. Например, что значит "разложить на два многочлена"? Написать формулу с заведомо целыми коэффициентами, зависящими от

и

? Или же найти все

, для каждого из которых можно указать конкретные

и

, допускающие разложение?
Например, вопрос: для каких натуральных

многочлен

можно разложить на линейные множители с целыми коэффициентами? Для чётных
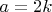
можно написать формулу

. Но если
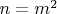
, то для любого

можно написать формулу

. И что отвечать?
Может быть стоит подробнее расписать условие задачи с кванторами для всех параметров? Это чисто дилетантское мнение

.