А вот тут я поискал и не нашёл (или начисто забыл). Можно попытаться говорить «тензорное произведение», в конце концов это частный случай именно его (

, где

— опускание (с помощью скалярного произведения) индекса у вектора, превращающее его в 1-форму — в индексной записи это всё будет
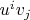
, ну и кстати как вы наверно в курсе, в бра-кет-обозначениях то же самое есть

, а такие произведения «без упрощения» (когда не умножается непосредственно бра на кет) как раз тензорные). В присутствии скалярного произведения все тензорные произведения двух множителей, «использующие» два вектора — кроме первого это

и ещё четыре с обратным порядком — будут приводимыми одно к другому). Может, кто-то и более точное название слышал.
-- Вт фев 25, 2020 21:14:04 --А, ну и да, вы же говорите о приближении оператора оператором ранга 1, и можно говорить «оператор ранга 1».
 -- Вт фев 25, 2020 21:19:04 --
-- Вт фев 25, 2020 21:19:04 --(Подобным образом вообще говорят о приближении произвольных тензоров тензорами ранга

— только не того ранга, который связан с валентностью, а того, который равен наименьшему числу слагаемых вида

, которые надо взять, чтобы в сумме получить такой тензор; для линейных операторов это совпадёт с их рангом.)