Ага, это у вас определение просто алгебры. А вот алгебры, получаемой из разбиения, какое?
Ну ладно, я сам предложу, а вы проверьте, что там такое же: алгебра, соответствующая разбиению

конечного

— это наименьшая алгебра, содержащая все

. Отсюда можно будет получить, что каждый элемент алгебры представляется в виде
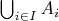
, где

; всего в такой алгебре

элементов, включая и пустое множество, и всё пространство, какое разбиение ни взять.
-- Сб фев 22, 2020 22:55:11 --
«Наименьшая алгебра» — содержащаяся в любой другой с тем же свойством. Хотя раз рассматривается конечное

, можно понимать более буквально — наименьшая по мощности.
Ну да, именно такое определение дается в Ширяеве. Только там нет ссылок на наименьшее множество. Просто строится соответствующее множество из
элементов. Давайте я перепишу доказательство из Ширяева, может я его неправильно понимаю.
Пусть

- некоторая алгебра подмножеств

. Тогда найдется и притом единственное разбиение

такое, что его элементы (атомы) являются элементами алгебры

и
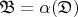
. В самом деле, пусть

и обладает тем свойством, что для всякого

множество

или совпадает с

или является пустым множеством. Тогда совокупность таких множеств

образует разбиение

с требуемым свойством
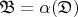
.