Отображение 2D волновой функции в 1D

[madschumacher]

Добрый день.

Вновь прошу прощения за беспокойство. Подскажите пожалуйста, какой самый простой и логичный способ можно взять, чтобы отобразить 2D волновую функцию $\psi(x,y)$ в 1D $\psi_{1D}(x)$.
Я брал следующие варианты:

• смотрел минимальные значения потенциала при каждом $x$, оттуда брал значение $y(x)$ и брал $\psi_{1D}(x)=\psi(x,y(x))$,
• находил минимум потенциала, брал значение $y_{\min}$, в котором оно возникало, и строил $\psi_{1D}(x) = \psi(x,y_{\min})$,
• брал интегралы $\psi_{1D}(x) = \int \psi(x,y) dy$ и $\psi_{1D}(x) = \int \psi(x,y) \cdot \exp\left( -\frac{(y - y_{\min})^2}{4\sigma^2} \right) dy$ с $\sigma$

Но что-то не то.

Есть ли какое-то более физически адекватное и понятное отображение 2D в 1D?

(Если кому интересно, вот они, волновые функции)

[Munin]

А в чём физический смысл того, что вы спрашиваете?

[madschumacher]

У меня имеются два сильно связанных колебания, я хочу классифицировать состояния по возбуждениям только одного из этих движений.

[Munin]

Вот это внятно. Спасибо. То есть, физически есть две степени свободы, а вас интересует одна из них.

В таком случае, берут

madschumacher в сообщении #1437395 писал(а):

$\psi_{1D}(x) = \int \psi(x,y) dy$

и называют это "проинтегрируем по одной степени свободы". (Предварительно можно сделать замену координат, типа $(x,y)\to(u,v).$ Для сильно связанных колебаний это может быть полезно.)

Но! Надо понимать, что это получится в итоге уже НЕ волновая функция. А именно:
- она будет отображать в каком-то смысле пространственное распределение вероятностей;
- она будет нормирована, как и исходная в.ф.;
- но она не будет подчиняться какому-то здравому динамическому уравнению;
- в частности для химиков, она не будет минимумом какого-то функционала.

[madschumacher]

Спасибо!

[g______d]

Munin в сообщении #1437428 писал(а):

- она будет нормирована, как и исходная в.ф.;

Нет, не будет (если только $\psi$ не константа по $y$, да даже и в этом случае нужно, чтобы по $y$ пространство было конечным, и нормировочный множитель).

[Munin]

Ох, да, и это не сохранится.

Прошу прощения, что соврал.

[madschumacher]

Munin в сообщении #1437428 писал(а):

"проинтегрируем по одной степени свободы"

По степени свободы хорошо работает в случаях чистых возбуждений по интересующей степени свободы:

В случае же возбуждения по второй оно даёт неправильный результат, очевидный невооружённым глазом:

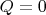
Состояние, очевидно, симметрично вдоль $Q=0$, но на одномерном отображении оно выглядит как дважды возбуждённое состояние.

Чтобы сгладить осцилляции по второй оси, я попробовал интегрировать, используя автокорреляционную функцию вдоль второй координаты в качестве веса при усреднении. И в этом случае ситуация исправляется для второго случая:

Но портится для некоторых вариантов первого:


Собственно, вот функция:

а вот её автокорреляция:


Может есть какой-то способ с этими случаями побороться одним средством?

[Munin]

Ваши "чистые" возбуждения далеко не "чистые", их надо долго "очищать", приводить к нормальным. К другим координатами, к разделяющимся переменным. Когда это будет достигнуто, тогда и то, что вы говорите, исправится. Пока это всего лишь симптом.

[upgrade]

madschumacher в сообщении #1437418 писал(а):

У меня имеются два сильно связанных колебания, я хочу классифицировать состояния по возбуждениям только одного из этих движений.

Один модулировать частотой (фазой), второй в смодулированном- амплитудой, и будет в одном сигнале информация о двух.

[madschumacher]

upgrade в сообщении #1437783 писал(а):

Один модулировать частотой (фазой), второй в смодулированном- амплитудой, и будет в одном сигнале информация о двух.

Я не очень понял, что Вы хотели этим сказать. Каких сигналах? Какую именно фазу (волновые функции тут действительные)? И главное, в каком месте то, что у меня получится по Вашему предложению, будет одномерным?

[mmadt]

madschumacher, если Вас интересует возможность описания состояния всей системы по состояниям одного из осцилляторов, рискну предположить, что это, в общем случае, невозможно. Если Вас просто не интересует, что происходит с одним из них и хочется иметь теоретическое описание состояний другого (в некотором выбранном базисе состояний), для этого обычно используют формализм "матрицы плотности". Некоторое общее описание Вы могли бы почерпнуть из "Ландау, Л. Д., Лифшиц, Е. М. Квантовая механика (нерелятивистская теория). — Издание 4-е. — М.: Наука, 1989. — 768 с. — («Теоретическая физика», том III). — ISBN 5-02-014421-5. — § 14". Описание на "русской" Википедии (https://ru.wikipedia.org/wiki/%D0%9C%D0 ... 1%82%D0%B8) более абстрактное, но там есть и другие ссылки. В целом, смысл "матрицы плотности" сводится к тому, что она позволяет вычислять средние значения произвольных наблюдаемых выбранной подсистемы квантовой системы. В некоторых случаях её можно интерпретировать, с некоторой натяжкой, как распределение вероятностей для выбранного базиса состояний.

[upgrade]

madschumacher в сообщении #1437787 писал(а):

Я не очень понял, что Вы хотели этим сказать. Каких сигналах? Какую именно фазу (волновые функции тут действительные)? И главное, в каком месте то, что у меня получится по Вашему предложению, будет одномерным?

Прошу прощения, прочитал только ваш второй пост и решил, что у вас гармонические колебания.