Наткнулся на метод. (случайно)
Если знать составные части числа K, то можно найти степень M для которого будет верно утверждение

Например
37*89*199=655307
K=655307
M=199440025800840449116009037576736768
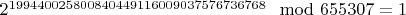
долго объяснять как получается M
но я подумал наверное эта тема известна
Практического смысла от этого нет, факторизация числа не решается эта задача :)
Знающие люди может посоветуют, что можно почитать по этой теме?
Наверное это простая задача на самом деле, и степень наверное не такая большая должна быть
-- Ср янв 22, 2020 19:14:37 --31*43*83*149=16485211
K=16485211
M=10422861155466402260340116655075422344733340627169947648000
