а основании BC равнобедренного треугольника ABC с углом при вершине в 100 градусов отмечена точка D такая, что AC=DC.
Затем через точку D проведена прямая, параллельная стороне AC, которая пересекает сторону AB в точке F.
Найти угол DCF.
Зная ответ, решение сочинить можно. Например, так (картинки я, увы, не умею рисовать)
Продолжим
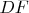
до пересечения в точке

с прямой, проходящей через

параллельно

: получим ромб
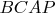
. Пусть его диагональ

пересекает

в точке

, а

- в точке

. Тогда угол

- прямой, а угол

равен
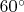
(считается). Значит,

(1)
Пусть

.
Из подобных тр-ков
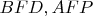
находим

(2)
Из подобных тр-ков

находим

откуда

(3),
а также

.
Учитывая (1) и (3), получим
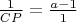
.
Но последнее вместе с (2) означает, что в тр-ке

прямая

есть биссектриса. Т.к. угол
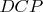
равен

, то искомый угол -

.....