Извиняюсь за долгое отсутствие.
Итак, подход, предложенный
nnosipov один из самых простых.
Прямо во время доказательства индукционного перехода, на этапе появления квадратного трехчлена можно доказать, что никакой

кроме

не подходит.

На вопросно-ответном сайте "Mathematics Stack Exchange"
предложили еще один хитрый способ. Суть ниже.
Предположим, что существует некое число

, которое тоже обращает наше неравенство в равенство:

Разобьем левую часть на два множителя:

Так как

, то для множителя
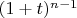
воспользуемся уже доказанным неравенством:

Умножим скобки друг на друга в правой части:

В итоге, с учетом нашего предположения, получаем следующее неравенство:

Из обеих частей этого неравенства вычитаем

:

Это неравенство не может быть истинным, так как

и

. Произведение слева всегда строго положительное число. Получили противоречие, а значит не существует такого

, кроме

, которое обращало бы неравенство в равенство при

.

Очень элегантно, как по мне.