Я бы сказал, что здесь есть как минимум три градации, а не две.
1) Счётно аддитивные заряды, абсолютно непрерывные по отношению к той мере, по которой рассматривается
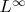
. В данном случае интегралы с функциями из

. Их можно определить напрямую.
2) Произвольные счётно аддитивные заряды конечной полной вариации. Их можно, как объяснил
demolishka, определить на

, а потом продолжить по Хану-Банаху на
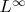
, не единственным образом.
3) Конечно, но не счётно аддитивные заряды. Пример: рассмотрим неглавный ультрафильтр на

. Объявим меру множества единицей если оно принадлежит ультрафильтру и нулём если не принадлежит. На самом деле это дельта-мера на одной из точек Стоун-Чеховской компактификации

. Очевидным образом эту меру (конечно-аддитивную) можно продолжить на подмножества

.
Прочитать о том, что такое ультрафильтр и как строить неглавные ультрафильтры с помощью леммы Цорна можно здесь:
https://en.wikipedia.org/wiki/Ultrafilterhttps://en.wikipedia.org/wiki/Boolean_p ... lter_lemmaВ каком месте в пункте 3 Хан-Банах -- я точно не знаю, потому что после того, как заряд построен, он определяет один функционал, а применение теоремы ХБ обычно предполагает какой-то произвол.
Возможно, заряд изначально строится как-то по-другому.