Прошу проверить мое доказательство следующего утверждения:
Утверждение.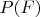
- векторное пространство всех полиномов над полем

.
Пусть

. Доказать, что тогда
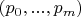
является базисом

.
Доказательство.Размерность пространства

равна

, векторов в кортеже
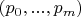
также

, поэтому мне просто нужно показать, что они линейно независимы и тогда они являются и базисом

.
Пусть

, где

это коэффициент у монома

-ой степени,

-го полинома.
Рассмотрим равенство их линейной комбинации нулю. Два полинома равны тогда и только тогда, когда равны их соответствующие коэффициенты.
Получим систему

Но у нас в каждой строке


не равен нулю, так как он берется из полинома

-й степени, а все стоящие справа от него слагаемые зануляются при обратном ходе метода Гаусса, слева же от него в уравнении ничего нет, так как у полинома
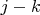
-й степени (

) все коэффициенты при мономах степени больше
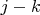
равны нулю. Таким образом из этой системы мы получаем, что
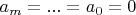
, а значит эти полиномы линейно независимы, значит они составляют базис

.
