Алгебраические расширения, соответствие Галуа.

[La Vie]

Я тут запутался.
Пусть $p,$ $q$ - простые целые числа, тогда легко показать, что $Q ( \sqrt{p})$ $\cap$ $Q (\sqrt{q}) = Q$. Оба расширения - расширения Галуа над $Q$ степени $2$, тогда их композит $Q (\sqrt{p}, \sqrt{q})$ - расширение Галуа над $Q$ степени $4$, с группой Галуа равной прямому произведению групп Галуа $Q ( \sqrt{p})$ и $Q ( \sqrt{q})$ над $Q$ - т.е. $V_4$.
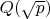
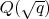
Значит, по соответствию Галуа имеется два нетривиальных промежуточных расширения между $Q (\sqrt{p}, \sqrt{q})$ и $Q$. Это собственно $Q( \sqrt{p} )$ и $Q( \sqrt{q} )$. У меня возникает вопрос по поводу расширения $Q( \sqrt{pq} )$. Оно, очевидно, содержится в построеном выше композите, вместе с тем не совпадает ни с одним из двух нетривиальных собственных промежуточных расширений.
Значит, оно должно совпадать с композитом. Но элемент $\sqrt{pq}$ имеет степень $2$ над $Q$, в то время как $deg$ $Q (\sqrt{p}, \sqrt{q} ) / Q$ $=4$.

[vpb]

Подумайте еще раз, сколько в $V_4$ подгрупп порядка 2.

[La Vie]

vpb
Действительно, их 3. Спасибо.

Ну, я рад, что это просто глупая ошибка, а то я начал бояться, что у меня какой-то фундаментальный баг в понимании.