vpbДо того как приступить к численным проверкам, хотелось бы понять теорему Паскаля.
Вот вы пишете:
То, что через каждую вторичную точку проходит по крайней мере 4 вторичных прямых --- это-то точно (собственно, из теоремы Паскаля тотчас следует...).
Можете это пояснить?

Касательно дальнейшего моделирования, предлагаю пронумеровать первичные точки как

, первичные прямые как

, вторичные точки как
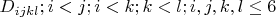
Как показано на рисунке. Как нумеровать вторичные прямые даже не знаю.
Так вот, исходя из этих обозначений, какие тройки вторичных точек по теореме Паскаля будут лежать на одной прямой?
Из рисунка я вижу, что числа в индексах точек, через которые проходит вторичная прямая (
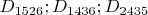
), повторяются два раза, то есть две единицы, две двойки, две тройки и т.п. Случайность?
Может, тут многое решится как-то комбинаторно?